题目内容
17.已知方程组$\left\{\begin{array}{l}{mx+n=5}\\{my-n=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,求m、n的值.分析 所谓“方程组”的解,指的是该数值满足方程组中的每一方程.只需把x、y的值代入原方程组,即可转化成关于m、n的二元一次方程组,进而求出m、n的值.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{mx+n=5}\\{my-n=1}\end{array}\right.$中,
可得:$\left\{\begin{array}{l}{m+n=5}\\{2m-n=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$,
m=2,n=3.
点评 此题考查方程组的解,本题所用的方法是待定系数法,在以后的学习中经常用来求函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
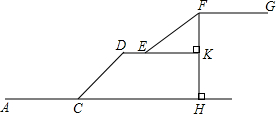 如图,校长寄语石到操场的垂直高度FH是30米,三教学楼到主席台的距离AC是60米,斜坡CD的坡脚是45°,斜坡EF的坡度i=3:4,公路宽DE与CH平行,且DE的延长线与FH的交点K,是FH中点,CH的长是40米,FG的长是50米.一名学生从三教学楼出发到行政楼交教学记录表,沿A-C-D-E-F-G路线,若上坡速度都为40米/分钟,平地速度都为50米/分钟,问该学生到达行政楼的时间是多少.($\sqrt{2}$≈1.4)
如图,校长寄语石到操场的垂直高度FH是30米,三教学楼到主席台的距离AC是60米,斜坡CD的坡脚是45°,斜坡EF的坡度i=3:4,公路宽DE与CH平行,且DE的延长线与FH的交点K,是FH中点,CH的长是40米,FG的长是50米.一名学生从三教学楼出发到行政楼交教学记录表,沿A-C-D-E-F-G路线,若上坡速度都为40米/分钟,平地速度都为50米/分钟,问该学生到达行政楼的时间是多少.($\sqrt{2}$≈1.4)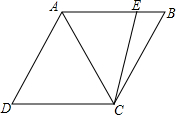 如图,在菱形ABCD中,AC=AB=4cm,点E是AB边上的动点,当BE=1cm时,作出线段CE绕点C逆时针旋转60°后,得到的线段CF,并求DF的长度.连接EF,当点E运动到什么位置时,△CEF周长有最小值?求出这个最小值.
如图,在菱形ABCD中,AC=AB=4cm,点E是AB边上的动点,当BE=1cm时,作出线段CE绕点C逆时针旋转60°后,得到的线段CF,并求DF的长度.连接EF,当点E运动到什么位置时,△CEF周长有最小值?求出这个最小值.
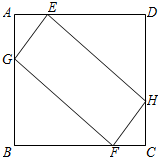 如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.
如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.