Question

4．已知，如图，△ABC．
（1）用尺规求作点P，使PA=PC，且点P到AC，BC的距离相等．（保留作图痕迹，不写作法）
（2）连接AP，若∠C=60°，AC=6，求点AP的长．

Answer 1

分析 （1）作AC的中垂线、∠ACB的角平分线，两线交点即为所求作点；
（2）过点P作PQ⊥AC于点Q，由角平分线可得∠ACP=∠BCP=$\frac{1}{2}$∠ACB=30°，根据等腰三角形性质知CQ=AQ=$\frac{1}{2}$AC=3，解直角三角形即可知PA=PC=$\frac{CQ}{cos∠ACP}$=2$\sqrt{3}$．

解答 解：（1）如图，点P即为所求；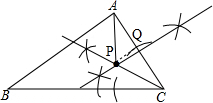


（2）过点P作PQ⊥AC于点Q，
∵PA=PC，
∴CQ=AQ=$\frac{1}{2}$AC=3，
又∵∠ACP=∠BCP=$\frac{1}{2}$∠ACB=30°，
∴CP=$\frac{CQ}{cos∠ACP}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$，
∴AP=2$\sqrt{3}$．

点评 本题主要考查角平分线的性质、中垂线的性质及作图，熟练掌握角平分线的性质、中垂线的性质及等腰三角形的性质是解题关键．