题目内容
5. 孔明老师出示了小黑板上的题后(如图),
孔明老师出示了小黑板上的题后(如图),①小赵说:“过点(3,0)”;
②小清说:“过点(4,3)”;
③小玲说:“a=1”;
④小斌说:“抛物线在x轴上截得的线段长为2”.
你认为四人的说法中,正确的说法有①②③④(填写序号)
分析 先利用对称性可确定抛物线与x轴的另一个交点为(3,0),再利用交点式可确定抛物线解析式得到a的值,然后判断点(4,3)在抛物线上,从而可判定四人的说法是否正确.
解答 解:由于抛物线y=ax2+bx+3的对称轴为直线x=2,而它与x轴的一个交点为(1,0),则它与x轴的另一个交点为(3,0),
所以抛物线解析式为y=a(x-1)(x-3),即y=ax2-4ax+3a,
则3a=3,解得a=1,
所以抛物线解析式为y=x2-4x+3,
当x=4时,y=16-16+3=3,
所以点(4,3)在抛物线上.
故答案为①②③④.
点评 本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系:△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
1.如果(-am)n=(-an)m,则( )
| A. | m为奇数,n为奇数 | B. | m为偶数,n为偶数 | C. | m,n奇偶性相同 | D. | m,n奇偶性相反 |
16.在函数y=$\frac{\sqrt{x}}{x-1}$中,自变量x的取值范围是( )
| A. | x≥1 | B. | x≤1且x≠0 | C. | x≥0且x≠1 | D. | x≠0且x≠1 |
13.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列说法中,正确的是( )
| A. | “打开电视,正在播放湖北新闻节目”是必然事件 | |
| B. | 某种彩票中奖概率为10%是指买十张一定有一张中奖 | |
| C. | “明天降雨的概率是50%表示明天有半天都在降雨” | |
| D. | “掷一次骰子,向上一面的数字是2”是随机事件 |
15.建科中学九(2)班5名同学在某一周零花钱分别为:30,25,25,40,35元,对于这组数据,以下说法中错误的是( )
| A. | 极差是15元 | B. | 平均数是31元 | C. | 众数是25元 | D. | 中位数是25元 |
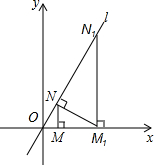 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M8坐标为(217,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M8坐标为(217,0).