Question

20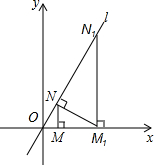．如图，已知直线l：y=$\sqrt{3}$x，过点M（2，0）作x轴的垂线交直线l于点N，过点N作直线l的垂线交x轴于点M₁；过点M₁作x轴的垂线交直线l于N₁，过点N₁作直线l的垂线交x轴于点M₂，…；按此作法继续下去，则点M₈坐标为（2¹⁷，0）．

Answer 1

分析 根据直线l的解析式求出∠MON=60°，从而得到∠MNO=∠OM₁N=30°，根据直角三角形30°角所对的直角边等于斜边的一半求出OM₁=2²•OM，然后表示出OM₆与OM的关系，再根据点M₈在x轴上写出坐标即可．

解答 解：∵直线l：y=$\sqrt{3}$x，
∴∠MON=60°，
∵NM⊥x轴，M₁N⊥直线l，
∴∠MNO=∠OM₁N=90°-60°=30°，
∴ON=2OM，OM₁=2ON=4OM=2²•OM，
同理，OM₂=2²•OM₁=（2²）²•OM，
…，
OM₈=（2²）⁸•OM=2¹⁶•2=2¹⁷，
所以，点M₈的坐标为（2¹⁷，0）．
故答案为：（2¹⁷，0）．

点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．