题目内容
15.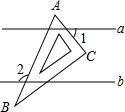 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
分析 如图,首先证明∠AMO=∠2;然后运用对顶角的性质求出∠ANM=55°,借助三角形外角的性质求出∠AMO即可解决问题.
解答  解:如图,∵直线a∥b,
解:如图,∵直线a∥b,
∴∠AMO=∠2;
∵∠ANM=∠1,而∠1=55°,
∴∠ANM=55°,
∴∠AMO=∠A+∠ANM=60°+55°=115°,
∴∠2=∠AMO=115°.
故选C.
点评 该题主要考查了平行线的性质、对顶角的性质、三角形的外角性质等几何知识点及其应用问题;牢固掌握平行线的性质、对顶角的性质等几何知识点是灵活运用、解题的基础.

练习册系列答案
相关题目
5. 如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为( )
如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为( )
 如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为( )
如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为( )| A. | 20 | B. | 22 | C. | 10 | D. | 14 |
3.在数轴上表示不等式2(1-x)<4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
10.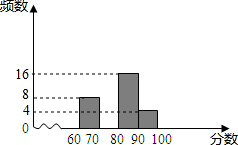 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
请根据图表提供的信息,解答下列问题:
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图| 分数段(分手为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x≤90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
(1)表中的a=12,b=40;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是108°;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为$\frac{2}{3}$.
7.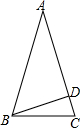 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )| A. | 36° | B. | 54° | C. | 18° | D. | 64° |
5.用配方法解一元二次方程x2-6x-4=0,下列变形正确的是( )
| A. | (x-6)2=-4+36 | B. | (x-6)2=4+36 | C. | (x-3)2=-4+9 | D. | (x-3)2=4+9 |
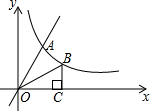 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.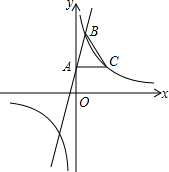 如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.
如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图: