题目内容
7．
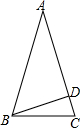如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（ ）| A． | 36° | B． | 54° | C． | 18° | D． | 64° |
分析 根据等腰三角形的性质由已知可求得∠A的度数，再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数．
解答 解：∵AB=AC，∠ABC=72°，
∴∠ABC=∠ACB=72°，
∴∠A=36°，
∵BD⊥AC，
∴∠ABD=90°-36°=54°．
故选：B．
点评 本题主要考查等腰三角形的性质，解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题，此题难度一般．
练习册系列答案
相关题目
正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图．
如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=$\frac{72}{5}$．在以上4个结论中，正确的有（ ）
15．
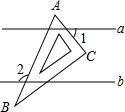如图，直线a∥b，一块含60°角的直角三角板ABC（∠A=60°）按如图所示放置．若∠1=55°，则∠2的度数为（ ）
如图，直线a∥b，一块含60°角的直角三角板ABC（∠A=60°）按如图所示放置．若∠1=55°，则∠2的度数为（ ）| A． | 105° | B． | 110° | C． | 115° | D． | 120° |
12．
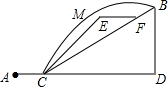如图所示，某同学的家在A处，书店在B处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（ ）
如图所示，某同学的家在A处，书店在B处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（ ）| A． | A→C→D→B | B． | A→C→F→B | C． | A→C→E→F→B | D． | A→C→M→B |
19．
如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（ ）
如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 150° |
如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD=3，AB=5，求$\frac{DE}{BC}$的值．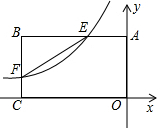
如图，反比例函数y=$\frac{k}{x}$（k＜0）的图象与矩形ABCD的边相交于E、F两点，且BE=2AE，E（-1，2）．