题目内容
已知:等边△ABC,D、E分别是射线AC、射线BC上的点,且∠BAE=∠CBD<60°,DH⊥AB点H.
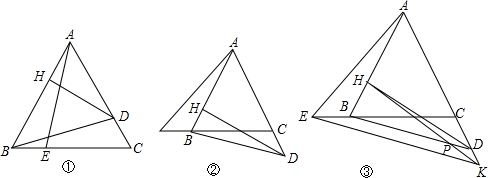
(1)如图1,当点D、E分别在边AC、边BC上时,求证:AC=2AH+BE;
(2)如图2,当点D、E分别在AC延长线和CB延长线上时,线段AC、AH、BE的数量关系为: ;
(3)在(2)的条件下,如图3,作EK∥BD交射线AC于点K,连接HK,交BC于点G,交BD于点P,当AC=6,BE=2时,求线段BP的长.

(1)如图1,当点D、E分别在边AC、边BC上时,求证:AC=2AH+BE;
(2)如图2,当点D、E分别在AC延长线和CB延长线上时,线段AC、AH、BE的数量关系为:
(3)在(2)的条件下,如图3,作EK∥BD交射线AC于点K,连接HK,交BC于点G,交BD于点P,当AC=6,BE=2时,求线段BP的长.
考点:相似形综合题
专题:
分析:(1)根据ASA,可得三角形全等,根据全等三角形性质,可得BE=CD,根据直角三角形的性质,可得AD与AH的关系,根据等量代换,可得答案;
(2)根据ASA,可得三角形全等,根据全等三角形性质,可得BE=CD,根据直角三角形的性质,可得AD与AH的关系,根据等量代换,可得答案;
(3)根据勾股定理,可得BD,根据相似三角形的判定与性质,可得CK、EK的长,根据等边三角形的判定与性质,可得BM=BH=HM=2,根据相似三角形的判定,可得
=
,根据相似三角形的性质,可得MG,再根据相似三角形的判定与性质,可得
=
,可得答案.
(2)根据ASA,可得三角形全等,根据全等三角形性质,可得BE=CD,根据直角三角形的性质,可得AD与AH的关系,根据等量代换,可得答案;
(3)根据勾股定理,可得BD,根据相似三角形的判定与性质,可得CK、EK的长,根据等边三角形的判定与性质,可得BM=BH=HM=2,根据相似三角形的判定,可得
| HM |
| KC |
| MG |
| CG |
| BP |
| EK |
| GB |
| GE |
解答:解:(1)如图1,

∵△ABC为等边三角形
∴∠ABC=∠C=∠CAB=60°,AB=BC,
∵∠BAE=∠CBD,
在△ABE和△BCD中,
,
∴△ABE≌△BCD(ASA),
∴BE=CD.
∵DH⊥AB,
∴∠DHA=90°
∵∠CAB=60°
∴∠ADH=30°,
∴AD=2AH,
∴AC=AD+CD=2AH+BE;
(2)AC+BE=2AH;
(3)如图2,作DS⊥BC延长线于点S,作HM∥AC交BC于点M,
∵AC=6,BE=2
∴由(2)得AH=4,BH=2
与(1)同理可得BE=CD=2,CE=8,
∵∠SCD=∠ACB=60°,
∴∠CDS=30°,
∴CS=1,SD=
,BS=7.
∵BD2=BS2+SD2=7 2+(
)2
∴BD=2
,
∵EK∥BD,
∴△CBD∽△CEK
∴
=
=
.
∴CK=
,EK=
.
∵HM∥AC,
∴∠HMB=∠ACB=60°
∴△HMB为等边三角形,BM=BH=HM=2,
CM=CB-BM=4,
∵HM∥AC,
∴∠MHG=∠CKG,∠HMG=∠KCG,
∴△HMG∽△KCG,
∴
=
,
即
=
,MG=
,BG=
,EG=
.
∵EK∥BD
∴△GBP∽△GEK,
∴
=
,
∴BP=
.

∵△ABC为等边三角形
∴∠ABC=∠C=∠CAB=60°,AB=BC,
∵∠BAE=∠CBD,
在△ABE和△BCD中,
|
∴△ABE≌△BCD(ASA),
∴BE=CD.
∵DH⊥AB,
∴∠DHA=90°
∵∠CAB=60°
∴∠ADH=30°,
∴AD=2AH,
∴AC=AD+CD=2AH+BE;
(2)AC+BE=2AH;
(3)如图2,作DS⊥BC延长线于点S,作HM∥AC交BC于点M,

∵AC=6,BE=2
∴由(2)得AH=4,BH=2
与(1)同理可得BE=CD=2,CE=8,
∵∠SCD=∠ACB=60°,
∴∠CDS=30°,
∴CS=1,SD=
| 3 |
∵BD2=BS2+SD2=7 2+(
| 3 |
∴BD=2
| 13 |
∵EK∥BD,
∴△CBD∽△CEK
∴
| CB |
| CE |
| CD |
| CK |
| BD |
| EK |
∴CK=
| 8 |
| 3 |
8
| ||
| 3 |
∵HM∥AC,
∴∠HMB=∠ACB=60°
∴△HMB为等边三角形,BM=BH=HM=2,
CM=CB-BM=4,
∵HM∥AC,
∴∠MHG=∠CKG,∠HMG=∠KCG,
∴△HMG∽△KCG,
∴
| HM |
| KC |
| MG |
| CG |
即
| 2 | ||
|
| MG |
| 4-MG |
| 12 |
| 7 |
| 26 |
| 7 |
| 40 |
| 7 |
∵EK∥BD
∴△GBP∽△GEK,
∴
| BP |
| EK |
| GB |
| GE |
∴BP=
26
| ||
| 15 |
点评:本题考查了相似形综合题,利用了全等三角形的判定与性质,直角三角形的性质,相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一组数据1,3,6,1,2的众数和中位数分别是( )
| A、1,6 | B、1,1 |
| C、2,1 | D、1,2 |
 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG, 某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表: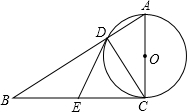 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.