题目内容
 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BF•BO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=
| ||
| 3 |
考点:圆的综合题
专题:几何综合题
分析:(1)连结OP,先由EP=EG,证出∠EPG=∠BGF,再由∠BFG=∠BGF+∠OBP=90°,推出∠EPG+∠OPB=90°来求证.
(2)连结OG,由BG2=BF•BO,得出△BFG∽△BGO,得出∠BGO=∠BFG=90°,根据垂径定理可得出结论.
(3)连结AC、BC、OG,由sinB=
,求出OG,由(2)得出∠B=∠OGF,求出OF,再求出BF,FA,利用直角三角形来求斜边上的高,再乘以2得出CD长度.
(2)连结OG,由BG2=BF•BO,得出△BFG∽△BGO,得出∠BGO=∠BFG=90°,根据垂径定理可得出结论.
(3)连结AC、BC、OG,由sinB=
| ||
| 3 |
解答:(1)证明:连结OP,

∵EP=EG,
∴∠EPG=∠EGP,
又∵∠EGP=∠BGF,
∴∠EPG=∠BGF,
∵OP=OB,
∴∠OPB=∠OBP,
∵CD⊥AB,
∴∠BFG=∠BGF+∠OBP=90°,
∴∠EPG+∠OPB=90°,
∴直线EP为⊙O的切线;
(2)证明:如图,连结OG,OP,

∵BG2=BF•BO,
∴
=
,
∴△BFG∽△BGO,
∴∠BGO=∠BFG=90°,
由垂径定理知:BG=PG;
(3)解:如图,连结AC、BC、OG、OP,

∵sinB=
,
∴
=
,
∵OB=r=3,
∴OG=
,
由(2)得∠EPG+∠OPB=90°,
∠B+∠BGF=∠OGF+∠BGF=90°,
∴∠B=∠OGF,
∴sin∠OGF=
=
∴OF=1,
∴BF=BO-OF=3-1=2,FA=OF+OA=1+3=4,
在Rt△BCA中,
CF2=BF•FA,
∴CF=
=
=2
.
∴CD=2CF=4
.

∵EP=EG,
∴∠EPG=∠EGP,
又∵∠EGP=∠BGF,
∴∠EPG=∠BGF,
∵OP=OB,
∴∠OPB=∠OBP,
∵CD⊥AB,
∴∠BFG=∠BGF+∠OBP=90°,
∴∠EPG+∠OPB=90°,
∴直线EP为⊙O的切线;
(2)证明:如图,连结OG,OP,

∵BG2=BF•BO,
∴
| BG |
| BO |
| BF |
| BG |
∴△BFG∽△BGO,
∴∠BGO=∠BFG=90°,
由垂径定理知:BG=PG;
(3)解:如图,连结AC、BC、OG、OP,

∵sinB=
| ||
| 3 |
∴
| OG |
| OB |
| ||
| 3 |
∵OB=r=3,
∴OG=
| 3 |
由(2)得∠EPG+∠OPB=90°,
∠B+∠BGF=∠OGF+∠BGF=90°,
∴∠B=∠OGF,
∴sin∠OGF=
| ||
| 3 |
| OF |
| OG |
∴OF=1,
∴BF=BO-OF=3-1=2,FA=OF+OA=1+3=4,
在Rt△BCA中,
CF2=BF•FA,
∴CF=
| BF•FA |
| 2×4 |
| 2 |
∴CD=2CF=4
| 2 |
点评:本题主要考查了圆的综合题,解题的关键是通过作辅助线,找准角之间的关系,灵活运用直角三角形中的正弦值.

练习册系列答案
相关题目
用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A、(x+
| ||||
B、(x+
| ||||
C、(x-
| ||||
D、(x-
|
 课本中有一道作业题:
课本中有一道作业题:
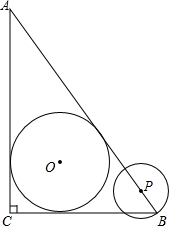 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= 如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF.
如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF. 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有