题目内容
6.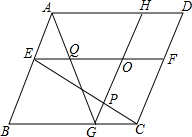 如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.
如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.
分析 先证明AD∥EF,GH∥CD,得出四边形AEFD、四边形CDHG、四边形AEOH、四边形CGOF是平行四边形,$\frac{OQ}{HA}$=$\frac{GO}{GH}$,$\frac{OP}{FC}$=$\frac{OE}{EF}$,得出AD=EF,CD=GH,HA=OE,OE=HA,证出EF=GH,得出AD=CD,即可得出结论.
解答  证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF,GH∥CD,
∴四边形AEFD、四边形CDHG、四边形AEOH、四边形CGOF是平行四边形,
$\frac{OQ}{HA}$=$\frac{GO}{GH}$,$\frac{OP}{FC}$=$\frac{OE}{EF}$,
∴AD=EF,CD=GH,HA=OE,OE=HA,
又∵OP=OQ,
∴EF=GH,
∴AD=CD,
∴?ABCD是菱形.
点评 本题考查了平行四边形的判定与性质、平行线的性质、菱形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
11. 已知如图,在△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BD的长为( )
已知如图,在△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BD的长为( )
 已知如图,在△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BD的长为( )
已知如图,在△ABC中,AB=AC=10,BD⊥AC于D,CD=2,则BD的长为( )| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
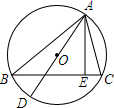 如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.
如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.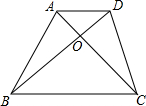 如图,梯形ABCD中,AD∥BC,对角线AC,BD交于点O,已知$\frac{AD}{BC}$=$\frac{2}{3}$,S△ACD=2,那么梯形ABCD的面积=5.
如图,梯形ABCD中,AD∥BC,对角线AC,BD交于点O,已知$\frac{AD}{BC}$=$\frac{2}{3}$,S△ACD=2,那么梯形ABCD的面积=5.