题目内容
1.为响应全民健身号召,甲、乙、丙三个户外骑行爱好者进行野外自行车骑行活动.甲从A城匀速骑行到B城,同时丙从B城匀速骑行到A城,丙的骑行速度小于甲的骑行速度,在丙出发30分钟时乙按照丙的骑行路线以甲的骑行速度赶往A城,设丙的骑行时间为t(单位:时),丙与甲、乙之间的距离为s(单位:千米),与t之间的函数关系如图①,图②所示,根据图象提供的信息解答下列问题:(1)A,B两城之间的距离为60千米;
(2)求图②中线段DE表示s与t之间的函数关系式,并写出自变量t的取值范围;
(3)乙与甲相遇时距离丙多远?
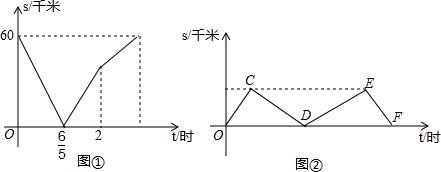
分析 (1)由图①可知,t=0时,s=60千米即为A,B两城之间的距离;
(2)由图①可知,甲行驶2小时到达B城,求出甲的速度,又t=$\frac{6}{5}$时甲、丙相遇,由此求出丙的速度,再由图②先求出C点坐标,得到D、E两点的坐标,利用待定系数法求出DE的解析式;
(3)先求出乙与甲相遇所需的时间,再分别求出此时丙与乙所行驶的路程,然后相减即可.
解答 解:(1)A,B两城之间的距离为60千米.
故答案为60;
(2)由图①可知,甲行驶2小时到达B城,则V甲=$\frac{60}{2}$=30(千米/时).
∵$\frac{6}{5}$(V甲+V丙)=60,即$\frac{6}{5}$(30+V丙)=60,
∴V丙=20(千米/时).
∵在丙出发30分钟时乙按照丙的骑行路线以甲的骑行速度赶往A城,丙的骑行时间为t(单位:时),丙与乙之间的距离为s(单位:千米),与t之间的函数关系如图②所示,
∴C($\frac{1}{2}$,10).
设乙用x小时追上丙,则(V乙-V丙)x=10,即(30-20)x=10,
解得x=1,
∵在D点时乙追上丙,
∴D($\frac{3}{2}$,0).
由图②可知,E($\frac{5}{2}$,10).
设DE的解析式为s=kt+b,
则$\left\{\begin{array}{l}{\frac{3}{2}k+b=0}\\{\frac{5}{2}k+b=10}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=10}\\{b=-15}\end{array}\right.$.
故s=10t-15($\frac{3}{2}$≤t≤$\frac{5}{2}$);
(3)设乙与甲相遇所需的时间是t,则(30+30)t=60-30×$\frac{1}{2}$,解得t=$\frac{3}{4}$,
此时丙已经行驶$\frac{1}{2}$+$\frac{3}{4}$=$\frac{5}{4}$(小时),
S丙=20×$\frac{5}{4}$=25(千米),S乙=30×$\frac{3}{4}$=$\frac{45}{2}$(千米),
S丙-S乙=25-$\frac{45}{2}$=$\frac{5}{2}$(千米).
点评 本题考查了一次函数的应用,行程问题中路程、速度与时间的关系,待定系数法求一次函数的解析式,利用图象获取信息的能力.掌握相遇与追及问题的等量关系是解题的关键.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案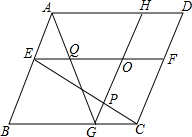 如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.
如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.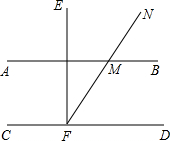 如图,AB∥CD,EF⊥CD于点F,射线FN交AB于点M,∠NMB=57°,则∠EFN=33°.
如图,AB∥CD,EF⊥CD于点F,射线FN交AB于点M,∠NMB=57°,则∠EFN=33°.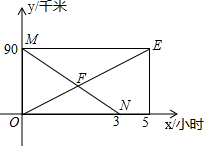 甲船从A港顺流到P港,乙船从P港逆流到A港,两船同时出发(两船在静水中速度相同),甲、乙两船与P港的距离y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题:
甲船从A港顺流到P港,乙船从P港逆流到A港,两船同时出发(两船在静水中速度相同),甲、乙两船与P港的距离y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题: