题目内容
15.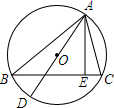 如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.
如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.
分析 因为AD是△ABC的外接圆直径,所以∠ABD=90°,根据∠BAD+∠D=90°,∠AEC=90°,可知∠D=∠ACB,所以∠BAD=∠CAE.
解答  证明:连接BD,
证明:连接BD,
∵AD是△ABC的外接圆直径,
∴∠ABD=90°.
∴∠BAD+∠D=90°.
∵AE是△ABC的高,
∴∠AEC=90°.
∴∠CAE+∠ACB=90°.
∵∠D=∠ACB,
∴∠BAD=∠EAC.
点评 此题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
18.若定义新运算a⊙b=2a-3b,则(x+y)⊙(x-y)的结果为( )
| A. | x-2y | B. | 2x-3y | C. | 5x-y | D. | 5y-x |
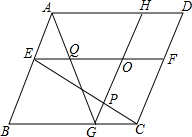 如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.
如图,己知O是?ABCD内一点,过O作GH∥AB分别交CB、AD于点G、H;过点O作EF∥BC分别交AB、CD于点E、F,联结CE交GH于点P,联结AG交EF于点Q,若OP=OQ,求证:?ABCD是菱形.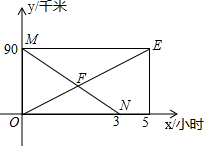 甲船从A港顺流到P港,乙船从P港逆流到A港,两船同时出发(两船在静水中速度相同),甲、乙两船与P港的距离y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题:
甲船从A港顺流到P港,乙船从P港逆流到A港,两船同时出发(两船在静水中速度相同),甲、乙两船与P港的距离y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题: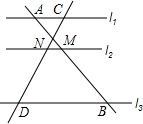 如图,l1∥l2∥l3,AM=2,MB=3,CD=4.5,则ND=2.7,CN=1.8.
如图,l1∥l2∥l3,AM=2,MB=3,CD=4.5,则ND=2.7,CN=1.8. 如图,在△ABC中,CA=CB,D,E分别是AB,AC边上的点,AD=AE,DE的延长线交BC的延长线于F点,DF=DB,求∠A的大小.
如图,在△ABC中,CA=CB,D,E分别是AB,AC边上的点,AD=AE,DE的延长线交BC的延长线于F点,DF=DB,求∠A的大小.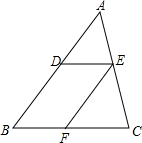 如图,已知在△ABC中,DE∥BC,EF∥AB,AE:EC=2:3,S△ABC=25,求S四边形BDEF.
如图,已知在△ABC中,DE∥BC,EF∥AB,AE:EC=2:3,S△ABC=25,求S四边形BDEF.