题目内容
17. 如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.
如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.
分析 利用锐角三角关系得出∠B=60°,再利用平行四边形的性质得出∠DAC的度数.
解答 解:∵在平行四边形ABCD中,BC=2AB,CA⊥AB,
∴cosB=$\frac{AB}{BC}$=$\frac{1}{2}$,
∴∠B=60°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD=120°,
∵∠BAC=90°,
∴∠DAC=30°.
故答案为:60,30.
点评 此题主要考查了平行四边形的性质以及锐角三角关系,熟练应用平行四边形的性质是解题关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
7.$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$是下列哪个二元一次方程组的解( )
| A. | $\left\{\begin{array}{l}{2x-y=-3}\\{4x+y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=-6}\\{2x+y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=-2}\\{x+2y=2}\end{array}\right.$ |
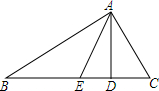 如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.
如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.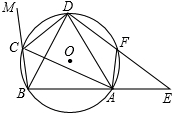 如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.
如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.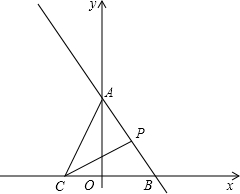 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.