题目内容
5.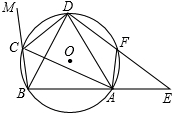 如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.
如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.(1)求证:△ABD为等腰三角形;
(2)若BC=AF,弧DF的度数为80°,求∠E的度数.
分析 (1)由CD为∠BCA的外角的平分线得到∠MCD=∠ACD,求出∠MCD=∠DAB推出∠DBA=∠DAB即可;
(2)由在△CDA与△FAE中,∠CDA=∠FAE,∠DCA=∠AFE,得出△DCA∽△FAE,得到∠E=∠DAC.
解答 证明:(1)∵四边形ABCD是圆O的内接四边形,
∴∠MCD=∠DAB,
∵CD为∠BCA的外角的平分线,
∴∠MCD=∠ACD,
∵∠DCA=∠DBA,
∴∠DAB=∠DBA,
∴DB=DA,
∴△ABD为等腰三角形;
(2)由(1)知AD=BD,BC=AF,则弧AFD=弧BCD,弧AF=弧BC,
∴∠BDC=∠ADF,弧CD=弧DF=40°,CD=DF,
∴∠BDC+∠BDA=∠ADF+∠BDA,
即∠CDA=∠BDF,
而∠FAE+∠BAF=∠BDF+∠BAF=180°,
∴∠FAE=∠BDF=∠CDA,
同理∠DCA=∠AFE.
在△DCA与△FAE中,
∠CDA=∠FAE,∠DCA=∠AFE,
∴△DCA∽△AFE,
∴∠E=∠DAC=40°.
点评 本题主要考查三角形外接圆和外心的概念,掌握圆内接四边形、相似三角形的性质和判定、圆周角定理等知识点是证此题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
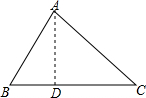 在△ABC中,BC=a,AC=b,AB=c;
在△ABC中,BC=a,AC=b,AB=c;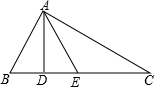 如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB.
如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB.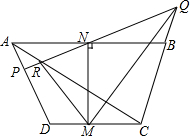 等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ.
等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ. 如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.
如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.