题目内容
9．因为$\left\{\begin{array}{l}x+y=4\\ 2x-y=-1\end{array}\right.$的解是$\left\{\begin{array}{l}{x=△}\\{y=△}\end{array}\right.$，所以一次函数y=-x+4与y=2x+1的图象交点坐标为（1，3）．分析 联立两函数解析式，解方程组即可求解．
解答 解：联立$\left\{\begin{array}{l}{y=-x+4}\\{y=2x+1}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$．
所以交点坐标为（1，3）．
故答案为：（1，3）．
点评 本题考查了两直线的交点的求解，联立两直线解析式解方程组即可，比较简单．
练习册系列答案
阅读快车系列答案
相关题目
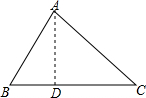在△ABC中，BC=a，AC=b，AB=c；
如图，在平行四边形ABCD中，BC=2AB，CA⊥AB，则∠B=60度，∠CAD=30度．
已知一次函数的图象经过点A（2，3），B（0，-2）．
两个一次函数y=5-x和y=2x-1的图象交点的坐标与方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解有什么关系？