题目内容
2.化简下列各式(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
(2)$\sqrt{27}$-4$\sqrt{\frac{1}{12}}$+$\sqrt{3}$
(3)$\frac{\sqrt{12}+\sqrt{27}}{\sqrt{3}}$-$\sqrt{\frac{1}{3}}$×$\sqrt{18}$
(4)($\sqrt{5}$-2)2-($\sqrt{3}$-2)($\sqrt{3}$+2)
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)根据二次根式的乘除法则运算;
(4)根据完全平方公式和平方差公式计算.
解答 解:(1)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(2)原式=3$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+$\sqrt{3}$
=$\frac{10\sqrt{3}}{3}$;
(3)原式=$\sqrt{\frac{12}{3}}$+$\sqrt{\frac{27}{3}}$-$\sqrt{\frac{1}{3}×18}$
=5-$\sqrt{6}$;
(4)原式=5-4$\sqrt{5}$+4-(3-4)
=9-4$\sqrt{5}$+1
=10-4$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
10.已知2是方程x2-ax+2=0的一个根,则方程的另一个根为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
 如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.
如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小. 如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.
如图,在平行四边形ABCD中,BC=2AB,CA⊥AB,则∠B=60度,∠CAD=30度.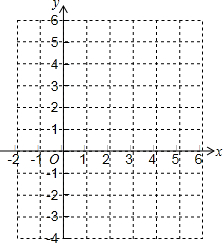 两个一次函数y=5-x和y=2x-1的图象交点的坐标与方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解有什么关系?
两个一次函数y=5-x和y=2x-1的图象交点的坐标与方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解有什么关系?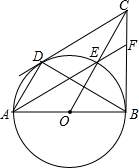 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )