题目内容
3.“黔北花海”是遵义的一个旅游景点,重庆北碚区游客欲前往观光,如果租2辆A型车和1辆B型车一次可载95人;租1辆A型车和2辆B型车一次可载100人.现计划同时租用A、B两种车型共5辆,一次载完160名游客.根据以上信息,解答下列问题:(1)一辆A型车和1辆B型车斗都坐满,A、B两种车型一次可分别载多少人?
(2)根据题中信息,请你设计用车方案;
(3)若A型车每辆需租金500元/次,B型车每辆需租金550元/次.请选出最省钱的租车方案,并求出最少租车费.
分析 (1)根据载客量,可得方程组,根据解方程组,可得答案;
(2)载客人数不小于160,车的辆数是非负数,可得答案;
(3)根据一次函数的性质,可得答案.
解答 解:设A型车可载x人,B型车可载y人,根据题意,得
$\left\{\begin{array}{l}{2x+y=95}\\{x+2y=100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=30}\\{y=35}\end{array}\right.$,
答:A、B两种车型一次可分别载30,35人;
(2)设A型车x辆,B型车(5-x)辆,根据题意,得
30x+35(5-x)≥160,
解得x≤3,
由车辆是非负数,得x≥0,
即0≤x≤3,
租车方案为:A型车0辆,B型车5辆;
A型车1辆,B型车4辆;
A型车2辆,B型车3辆;
A型车3辆,B型车2辆;
(3)设A型车x辆,B型车(5-x)辆,根据题意,得
租车费用为y=500x+550(5-x),
化简,得
y=-50x+2750
k=-50<0,y随x的增大而减小,
当x=3时,y最小=2600元,
租A型车3辆,B型车2辆,最少租车费用是2600元.
点评 本题考查了一次函数的应用,解(1)的关键是解方程组;解(2)的关键是解不等式组;解(3)的关键是利用一次函数的性质.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
11.班上有男女生共41人,女生人数的一半比男生总数少8人,该班女生人数是( )
| A. | 20人 | B. | 21人 | C. | 22人 | D. | 23人 |
8.用A、B两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如表:
(1)若要配制这种饮料10千克,要求至少含有4000单位的维生素C,试求出所需A种原料最少多少千克?
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
| 原料 维生素及价格 | A种原料 | B种原料 |
| 维生素C(单位/千克) | 600 | 100 |
| 原料价格(元/千克) | 6 | 4 |
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
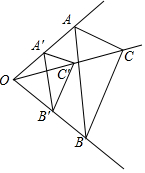 如图,若△A'B'C'与△ABC位似,相似比为k.
如图,若△A'B'C'与△ABC位似,相似比为k. 如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB方向平移得到△DEF,若四边形ABED的面积等于8,则平移的距离为2.
如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB方向平移得到△DEF,若四边形ABED的面积等于8,则平移的距离为2.