题目内容
15.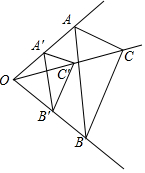 如图,若△A'B'C'与△ABC位似,相似比为k.
如图,若△A'B'C'与△ABC位似,相似比为k.(1)因为$\frac{OA'}{OA}=\frac{OC'}{OC},∠A'OC'=∠AOC$,
所以△A′OC′∽△AOC.
所以$\frac{OA'}{OA}=\frac{OC'}{OC}=\frac{A'C'}{AC}$=k,同理,$\frac{OB'}{OB}$=k.
归纳:在位似形中,各对应点到位似中心的距离之比等于相似比.(注意:对应点重合除外)
(2)因为$\frac{OA'}{OA}=\frac{OC'}{OC}$,∠A'OC'=∠AOC,
所以△A′OC′∽△AOC.
所以∠OA′C′=∠OAC.
所以A'C'∥AC,同理,B'C'∥BC,A'B'∥AB.
归纳:在位似形中,各对应边互相平行.(注意:对应边所在的直线重合出完)
分析 根据相似三角形的性质、位似变换的概念和性质解答.
解答 解:(1)因为$\frac{OA'}{OA}=\frac{OC'}{OC},∠A'OC'=∠AOC$,
所以△A′OC′∽△AOC.
所以$\frac{OA'}{OA}=\frac{OC'}{OC}=\frac{A'C'}{AC}$=k,同理,$\frac{OB'}{OB}$=k.
归纳:在位似形中,各对应点到位似中心的距离之比等于相似比.(注意:对应点重合除外)
(2)因为$\frac{OA'}{OA}=\frac{OC'}{OC}$,∠A'OC'=∠AOC,
所以△A′OC′∽△AOC.
所以∠OA′C′=∠OAC.
所以A'C'∥AC,同理,B'C'∥BC,A'B'∥AB.
归纳:在位似形中,各对应边互相平行.
故答案为:(1)A′OC′;AOC;k;k;相似比;
(2)A′OC′;AOC;OA′C′;OAC;∥;∥;∥;互相平行.
点评 本题考查的是位似变换的概念和性质,掌握位似图形的定义:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
| A绳子 | B绳子 | C绳子 | |
| 长度(米) | 8 | 6 | 4 |
| 单价(元/条) | 12 | 8 | 6 |
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
 如图,三角板的直角顶点在直线l上,若∠1=70°,则∠2=20°.
如图,三角板的直角顶点在直线l上,若∠1=70°,则∠2=20°.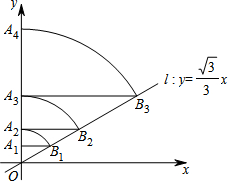 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=22016.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=22016.