题目内容
 如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.(1)求证:GF=BF;
(2)若△ABC的边长为a,BE的长为b,且a,b满足(a-7)2+b2-6b+9=0,求BF的长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)由DG∥BE得到∠GDF=∠E,则可根据“AAS”判定△FDG≌△FEB,则GF=BF;
(2)利用配方法得(a-7)2+(b-3)2=0,则根据非负数的性质得到a-7=0,b-3=0,解得a=7,b=3,即BE=3,BC=7,所以DG=BE=3,由于DG∥AB,△ABC是等边三角形,则△CDG为等边三角形,所以CG=DG=3,可计算出BG=BC-CG=4,然后利用GF=BF可得到BF的长.
(2)利用配方法得(a-7)2+(b-3)2=0,则根据非负数的性质得到a-7=0,b-3=0,解得a=7,b=3,即BE=3,BC=7,所以DG=BE=3,由于DG∥AB,△ABC是等边三角形,则△CDG为等边三角形,所以CG=DG=3,可计算出BG=BC-CG=4,然后利用GF=BF可得到BF的长.
解答:(1)证明:∵DG∥BE,
∴∠GDF=∠E,
在△FDG和△FEB中,
,
∴△FDG≌△FEB(AAS),
∴GF=BF;
(2)解:∵(a-7)2+b2-6b+9=0,
∴(a-7)2+(b-3)2=0,
∴a-7=0,b-3=0,解得a=7,b=3,
∴BE=3,BC=7,
∴DG=BE=3,
∵DG∥AB,
∴△CDG为等边三角形,
∴CG=DG=3,
∴BG=BC-CG=4,
而GF=BF,
∴BF=
BG═2.
∴∠GDF=∠E,
在△FDG和△FEB中,
|
∴△FDG≌△FEB(AAS),
∴GF=BF;
(2)解:∵(a-7)2+b2-6b+9=0,
∴(a-7)2+(b-3)2=0,
∴a-7=0,b-3=0,解得a=7,b=3,
∴BE=3,BC=7,
∴DG=BE=3,
∵DG∥AB,
∴△CDG为等边三角形,
∴CG=DG=3,
∴BG=BC-CG=4,
而GF=BF,
∴BF=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了等边三角形的性质.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
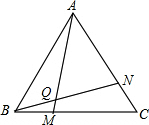 △ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.
△ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.
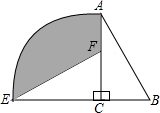 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=