题目内容
16. 如图,AB是⊙O的直径,BC是⊙O的弦,OD⊥CB于点E,交BC于点E.
如图,AB是⊙O的直径,BC是⊙O的弦,OD⊥CB于点E,交BC于点E.(1)请写出三个不同类型的正确结论;
(2)连接CD,∠ABC=20°,求∠CDE的度数.
分析 (1)根据圆周角定理和垂径定理回答即可;
(2)先求得∠CAB=70°,由圆内接四边形的性质可知∠CDB=110°,然后由∠CDE=$\frac{1}{2}∠$CDB求解即可.
解答 解:(1)①∠ACB=90°②CE=EB,③CD=BD.
理由:∵AB是圆O的直径,
∴∠ACB=90°.
∵OD⊥BC,
∴CE=EB,$\widehat{CD}=\widehat{BD}$.
∵$\widehat{CD}=\widehat{BD}$,
∴CD=BD.
(2)如图所示: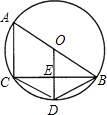
∵AB是圆O的直径,
∴∠ACB=90°.
∴∠A=90°-20°=70°.
∵四边形ABDC是圆内接四边形,
∴∠A+∠CDB=180°.
∴∠CDB=110°.
由(1)可知CD=DB.
又∵OD⊥BC,
∴∠CDE=$\frac{1}{2}∠$CDB=$\frac{1}{2}×110°$=55°.
点评 本题主要考查的是垂径定理、圆周角定理的应用,利用圆内接四边形的性质求得∠CDB的度数是解题的关键.

练习册系列答案
相关题目
4.一个多边形从一个顶点出发共引7条对角线,那么这个多边形对角线的总数为( )
| A. | 70 | B. | 35 | C. | 45 | D. | 50 |
 如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC. 已知:△ABC中,AB、AC的垂直平分线分别交BC于点M、N.AB=4,AC=7,BC=10.求:△AMN的周长.
已知:△ABC中,AB、AC的垂直平分线分别交BC于点M、N.AB=4,AC=7,BC=10.求:△AMN的周长.