题目内容
1.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
分析 (1)首先设甲店B型产品有(70-x),乙店A型有(40-x)件,B型有(x-10)件,列出不等式方程组求解即可;
(2)由(1)的解析式和x的取值范围可得几种不同的分配方案.
解答 解:依题意,分配给甲店A型产品x件,则甲店B型产品有(70-x)件,乙店A型有(40-x)件,B型有{30-(40-x)}件,则
(1)W=200x+170(70-x)+160(40-x)+150(x-10)=20x+16800.
由$\left\{\begin{array}{l}{x≥0}\\{70-x≥0}\\{40-x≥}\\{x-10≥0}\end{array}\right.$,
解得10≤x≤40.
(2)由W=20x+16800≥17560,
∴x≥38.
∴38≤x≤40,x=38,39,40.
∴有三种不同的分配方案.
方案一:x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件;
方案二:x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件;
方案三:x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件.
点评 本题主要考查利用一次函数的实际应用问题与不等式组的求解方法.此题难度适中,解题的关键是理解题意,掌握一次函数的性质应用.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
13.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a6÷a2=a3 | C. | a2+a3=a5 | D. | (a3)2=a6 |
11. 如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
 如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
如图,在正方形网格中,∠1、∠2、∠3的大小关系( )| A. | ∠1=∠2=∠3 | B. | ∠1<∠2<∠3 | C. | ∠1=∠2>∠3 | D. | ∠1<∠2=∠3 |
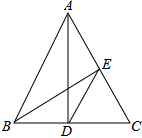 已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.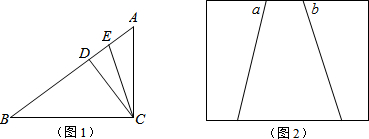
 如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.