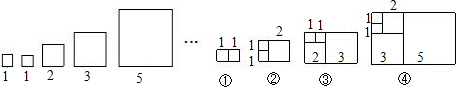题目内容
11. 如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
如图,在正方形网格中,∠1、∠2、∠3的大小关系( )| A. | ∠1=∠2=∠3 | B. | ∠1<∠2<∠3 | C. | ∠1=∠2>∠3 | D. | ∠1<∠2=∠3 |
分析 由平行线的性质可知:∠CBD=∠BDE,∠EDF=∠DFG,然后根据锐角三角形函数的定义可知:tan∠ABC=$\frac{1}{3}$,tan∠EDF=$\frac{2}{3}$,tan∠BDE=tan∠GFH=$\frac{1}{2}$,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
解答 解:如图所示:
根据图形可知:
∠CBD=∠BDE,tan∠ABC=$\frac{1}{3}$,tan∠EDF=$\frac{2}{3}$,
∴∠ABC<∠EDF
∴∠ABC+∠CBD<∠EDF+∠BDE,即∠1<∠2.
根据图形可知:∠EDF=∠DFG,tan∠BDE=$\frac{2}{4}=\frac{1}{2}$,tan∠GFH=$\frac{1}{2}$,
∴∠BDE=∠GFH.
∴∠EDF+∠BDE=∠DFG+∠GFH,即:∠2=∠3.
故选:D.
点评 本题主要考查的是锐角三角函数的增减性和平行线的性质,根据正切函数的增减性判定出∠ABC<∠EDF,∠BDE=∠GFH是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
2.若a=($\frac{3}{2}$)-2,b=(-1)-1,c=($\frac{π}{2}$)0,则a、b、c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
3.已知多项式x2+a能用平方差公式在有理数范围内分解因式,那么在下列四个数中a可以等于( )
| A. | 9 | B. | 4 | C. | -1 | D. | -2 |
 老师在上概率课时,邀请小明和小华两名同学来做游戏,要求:小明用不透明的白布包住三根同样颜色、长短的细绳AA1、BB1、CC1,只露出它们的头和尾,(如图所示).
老师在上概率课时,邀请小明和小华两名同学来做游戏,要求:小明用不透明的白布包住三根同样颜色、长短的细绳AA1、BB1、CC1,只露出它们的头和尾,(如图所示).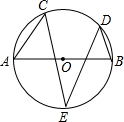 如图,AB是⊙O的直径,C、D、E都是⊙O上的点,∠A=55°,∠B=70°,则∠E的度数是35°.
如图,AB是⊙O的直径,C、D、E都是⊙O上的点,∠A=55°,∠B=70°,则∠E的度数是35°.