题目内容
12.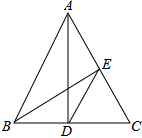 已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
分析 利用三角形面积以及锐角三角函数关系和三角形中位线定理分别分析得出即可.
解答 解:∵AD⊥BC于D,BE⊥AC于E,
∴$\frac{1}{2}$BE•AC=$\frac{1}{2}$AD•BC,
∴BE•AC=AD•BC,
∴$\frac{AC}{BC}$=$\frac{AD}{BE}$,
故①正确;
无法得出AE•BE=AD•BD,故②错误;
∵∠C=60°,AD⊥BC于D,BE⊥AC于E,
∴cosC=$\frac{CD}{AC}$=$\frac{EC}{BC}$,
∴$\frac{CD}{CE}$=$\frac{AC}{BC}$,故③正确;
由AD⊥BC,BE⊥AC可得∠CEB=∠CDA=90°,∠C=∠C,
所以△CAD∽△CBE,
则$\frac{CE}{BC}$=$\frac{CD}{AC}$
所以△CDE∽△CAB,
所以$\frac{CD}{CA}$=$\frac{CE}{BC}$=$\frac{DE}{AB}$,
又因为∠C=60°,
所以CE:CB=1:2,
所以AB=2DE,故④正确.
故答案为:①③④.
点评 此题主要考查了三角形面积以及锐角三角函数关系和三角形中位线定理等知识,正确利用比例式的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知等腰三角形一边长为3,一边长为2,则这个三角形周长为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 7或8 |
1.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
2.若a=($\frac{3}{2}$)-2,b=(-1)-1,c=($\frac{π}{2}$)0,则a、b、c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
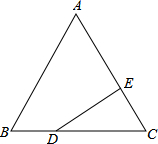 等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.
等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.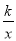 的图象经过点A(1,
的图象经过点A(1, 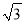 ).
).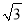 ,1)是否在此反比例函数的图象上,并说明理由.
,1)是否在此反比例函数的图象上,并说明理由.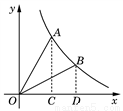
 B.
B.  C.
C.  D.
D.