题目内容
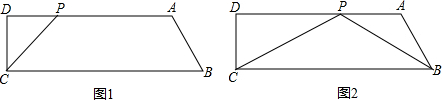
16.(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=5,AC=3,CE平分∠ACD,求BE的长;(2)小明完成(1)后,联想到如下问题:已知一个角的两边是a和b,顶点在矩形图纸外面(如图2),请用直尺和圆规在矩形图纸内作出这个角的平分线.(注:直尺没有刻度!作图不要求写作法,但要保留作图痕迹,并对作图中涉及的点用字母进行标注.作图过程中如果要突破矩形图纸限制,可适当延伸,但不得使a、b相交.)
爱动脑筋的你一起来完成这个作图吧!
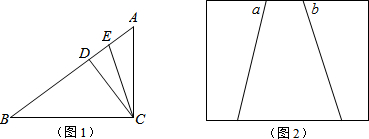
分析 (1)作EM⊥AC交AC于点M,利用勾股定理求出BC,再利用△ACD∽△ABC,得出$\frac{EM}{AE}$=$\frac{BC}{AB}$,可解得AD的值,由角平分线定理可得EM=DE,联立可解出AE的值,利用BE=AB-AE即可求解,
(2)延长两边分别作两组角的平分线,连接平分线的两个交点所在的线就是这个角的平分线.
解答 解:(1)如图1,作EM⊥AC交AC于点M,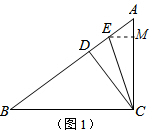
∵Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=5,AC=3,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵△ACD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即$\frac{AD}{3}$=$\frac{3}{5}$,解得AD=$\frac{9}{5}$,
∵∠ABC=∠AEM,
∴$\frac{EM}{AE}$=$\frac{BC}{AB}$,即$\frac{EM}{AE}$=$\frac{4}{5}$,
∵CE平分∠ACD,CD⊥AB,EM⊥AC,
∴EM=DE,
∴$\frac{DE}{AE}$=$\frac{4}{5}$且DE+AE=$\frac{9}{5}$,解得DE=$\frac{4}{5}$,AE=1,
∴BE=AB-AE=5-1=4.
(2)如图2,延长两边分别作两组角的平分线,连接平分线的两个交点所在的线就是这个角的平分线.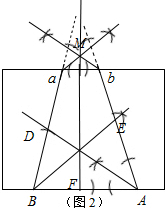
点评 本题主要考查了作图,角平分线的性质及勾股定理,解题的关键是理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.

练习册系列答案
相关题目
4.已知等腰三角形一边长为3,一边长为2,则这个三角形周长为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 7或8 |
11.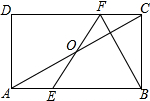 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
1.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来.
 如图所示,已知AB∥EF∥CD,AC,BD相交于点E,AB=3cm,CD=6cm,则EF=2cm.
如图所示,已知AB∥EF∥CD,AC,BD相交于点E,AB=3cm,CD=6cm,则EF=2cm.