题目内容
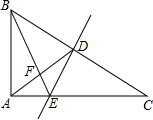 已知,如图,在Rt△ABC中,∠BAC=90°,BC的垂直平分线DE分别交BC、AC于点D、E,BE和AD相交于点F,设∠AFB=y,∠C=x.
已知,如图,在Rt△ABC中,∠BAC=90°,BC的垂直平分线DE分别交BC、AC于点D、E,BE和AD相交于点F,设∠AFB=y,∠C=x.(1)求证:∠CBE=∠CAD;
(2)求y与x的函数关系式;
(3)写出函数的定义域.
考点:线段垂直平分线的性质,函数关系式,函数自变量的取值范围
专题:
分析:(1)先根据垂直平分线的性质得出BE=CE,故∠CBE=∠C=x.再由D为BC的中点可知AD=DC,故∠CAD=∠C=x,由此可得出结论;
(2)由(1)知,∠CBE=∠CAD=∠C=x,根据三角形外角的性质可得∠ADB=2x,同理可得出结论;
(3)由直角三角形的性质可得出结论.
(2)由(1)知,∠CBE=∠CAD=∠C=x,根据三角形外角的性质可得∠ADB=2x,同理可得出结论;
(3)由直角三角形的性质可得出结论.
解答:(1)证明:∵DE垂直平分BC,
∴BE=CE,
∴∠CBE=∠C=x.
∵∠A=90°,D为BC的中点,
∴AD=DC,
∴∠CAD=∠C=x,
∴∠CBE=∠CAD;
(2)解:∵由(1)知,∠CBE=∠CAD=∠C=x,
∴∠ADB=2x,
∵∠AFB=∠EBD+∠ADB,
∴y=3x.
(3)解:∵∠C+∠ABC=90°,∠CBE=∠CAD,
∴0°<x<45°.
∴BE=CE,
∴∠CBE=∠C=x.
∵∠A=90°,D为BC的中点,
∴AD=DC,
∴∠CAD=∠C=x,
∴∠CBE=∠CAD;
(2)解:∵由(1)知,∠CBE=∠CAD=∠C=x,
∴∠ADB=2x,
∵∠AFB=∠EBD+∠ADB,
∴y=3x.
(3)解:∵∠C+∠ABC=90°,∠CBE=∠CAD,
∴0°<x<45°.
点评:本题考查的是线段垂直平分线的性质,用到的知识点为:线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4的平方根是( )
| A、2 | ||
B、
| ||
| C、±2 | ||
D、±
|
 今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时)
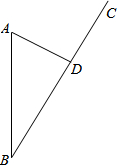
今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时) 如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C.
如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.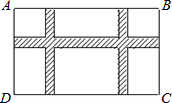 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是