题目内容
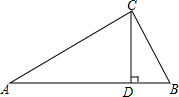 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:锐角三角函数的定义
专题:
分析:根据勾股定理,可得AB,根据余角的性质,可得∠ACD=∠B,再根据等角的三角函数相等,可得答案.
解答:解:在Rt△ABC中,∠ACB=90°,由勾股定理,得
AB=
=
=
,
由余角的性质,得∠ACD=∠B,
由正弦函数的定义,得
sin∠ACD=sin∠B=
=
=
,
故选:B.
AB=
| AC2+BC2 |
| 22+12 |
| 5 |
由余角的性质,得∠ACD=∠B,
由正弦函数的定义,得
sin∠ACD=sin∠B=
| AC |
| AB |
| 2 | ||
|
2
| ||
| 5 |
故选:B.
点评:本题考查了锐角三角函数的定义,利用了勾股定理,余角的性质,正弦三角函数等对边比斜边.

练习册系列答案
相关题目
 如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )
如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )| A、30° | B、25° |
| C、20° | D、15° |
在2.5,-2.5,0,2这四个数中,最小的一个数是( )
| A、2.5 | B、-2.5 | C、0 | D、2 |
 如图∠1与∠2是同位角,∠2与∠3是同位角,因此∠1与∠3是同位角,对吗?为什么?你是怎么来判断同位角的?
如图∠1与∠2是同位角,∠2与∠3是同位角,因此∠1与∠3是同位角,对吗?为什么?你是怎么来判断同位角的? 如图,点D是△ABC的外接圆的弧
如图,点D是△ABC的外接圆的弧
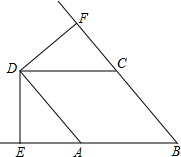 如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.
如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形. 如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C.
如图,已知Rt△ABC,∠BAC=90°,点D在BC上,AD=DC,DE⊥AB,交AB于O,BE∥AD.求证:∠BED=∠C. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.