题目内容
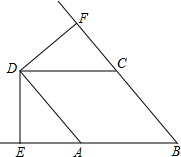
如图,∠1=50°,则∠A+∠B+∠C+∠D+∠E+∠F=


考点:三角形的外角性质
专题:
分析:首先根据邻补角的性质可得∠2的度数,再根据三角形内角和外角的性质可得∠A+∠B=∠3,∠3+∠C=∠4,∠F+∠4=∠2,∠D+∠E=∠2,进而可得答案.
解答: 解:∵∠1=50°,
解:∵∠1=50°,
∴∠2=130°,
∵∠A+∠B=∠3,∠3+∠C=∠4,∠F+∠4=∠2,
∴∠A+∠B+∠C+∠F=∠2=130°,
∵∠D+∠E=∠2=130°,
∴∠A+∠B+∠C+∠D+∠E+∠F=260°,
故答案为:260°.
 解:∵∠1=50°,
解:∵∠1=50°,∴∠2=130°,
∵∠A+∠B=∠3,∠3+∠C=∠4,∠F+∠4=∠2,
∴∠A+∠B+∠C+∠F=∠2=130°,
∵∠D+∠E=∠2=130°,
∴∠A+∠B+∠C+∠D+∠E+∠F=260°,
故答案为:260°.
点评:此题主要考查了三角形内角和外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
4的平方根是( )
| A、2 | ||
B、
| ||
| C、±2 | ||
D、±
|
周末,小军(用A表示)、小明(用B表示)、小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁有四个座位,A先坐下来,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而坐的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
用科学记数方法表示0.0000908,得( )
| A、9.08×10-5 |
| B、9.08×10-4 |
| C、90.8×10-6 |
| D、90.8×10-7 |
 如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.
如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.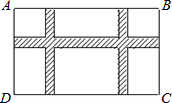 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,若通道的宽设计成xm,则阴影部分的面积是 如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.
如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.