题目内容
11. 如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为
如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为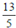 .
.
分析 作AF⊥BC于F,连接AD,设AF=a,DC=x,根据相似三角形的性质用a表示CD和BD,计算即可.
解答 解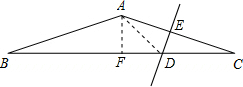 :作AF⊥BC于F,连接AD,
:作AF⊥BC于F,连接AD,
设AF=a,DC=x,
∵tan∠B=$\frac{1}{3}$,
∴BF=3a,
由勾股定理得,AB=$\sqrt{10}$a,
∵DE⊥AC,AF⊥BC,
∴△CED∽△CFA,
∴$\frac{CE}{CF}$=$\frac{CD}{CA}$,即$\frac{\frac{\sqrt{10}a}{2}}{3a}$=$\frac{x}{\sqrt{10}a}$,
解得x=$\frac{5}{3}$a,
∴DF=CF-CD=$\frac{4}{3}$a,
∴BD=$\frac{13}{3}$a,
∴$\frac{BD}{DC}$=$\frac{13}{5}$.
故答案为:$\frac{13}{5}$.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
2. 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )| A. | 点E | B. | 点F | C. | 点P | D. | 点Q |
6.下列四个命题,其中真命题有( )
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.化简$\sqrt{\frac{1}{8}}$,其结果是( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{8}}}{8}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | ±$\frac{{\sqrt{2}}}{4}$ |
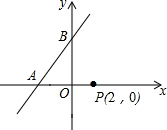 如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.
如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.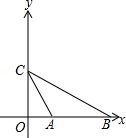 如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);
如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);