��Ŀ����
��֪������y=x2-(m+1)x+m��
��1����֤����������x��һ���н��㣻
��2������������x�ύ��A(x1,0����B��x2,0�����㣬x1��0��x2,��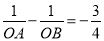 ,��m��ֵ.
,��m��ֵ.
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��Ŀ����
��֪������y=x2-(m+1)x+m��
��1����֤����������x��һ���н��㣻
��2������������x�ύ��A(x1,0����B��x2,0�����㣬x1��0��x2,��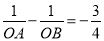 ,��m��ֵ.
,��m��ֵ.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�