题目内容
9. 有这样一个问题:探究函数y=$\frac{{x}^{2}-1}{x}$的图象与性质:
有这样一个问题:探究函数y=$\frac{{x}^{2}-1}{x}$的图象与性质:小宏根据学习函数的经验,对函数y=$\frac{{x}^{2}-1}{x}$的图象与性质进行了探究.
下面是小宏的探究过程,请补充完整:
(1)函数y=$\frac{{x}^{2}-1}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{3}{2}$ | 0 | m | $\frac{8}{3}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | 0 | $\frac{3}{2}$ | n | … |
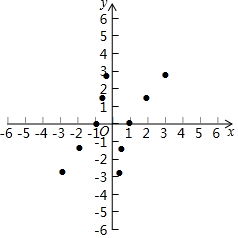
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(两条即可):①x<0时,函数y随x的增大而增大.②x>0时,函数y随x的增大而增大..
分析 (1)根据分母不能为0即可写出自变量的取值范围、
(2)分别求出x=-$\frac{1}{2}$、3时的函数值即可.
(3)利用描点法即可画出图象,观察图象可得函数的性质.
(4)利用图象写两个性质即可.
解答 解:(1)数y=$\frac{{x}^{2}-1}{x}$的自变量x的取值范围x≠0,
故答案为x≠0.
(2)当x=-$\frac{1}{2}$时,m=$\frac{(-\frac{1}{2})^{2}-1}{-\frac{1}{2}}$=$\frac{3}{2}$,
当x=3时,n=$\frac{{3}^{2}-1}{3}$=$\frac{8}{3}$.
(3)函数图象如图所示,
(4)性质①x<0时,函数y随x的增大而增大.
②x>0时,函数y随x的增大而增大.
故答案为:x<0时,函数y随x的增大而增大;为x>0时,函数y随x的增大而增大.
点评 本题考查函数的图象一个的问题,解题的关键是确定函数自变量的取值范围,学会用描点法画函数图象,能观察图象,总结函数的性质,属于中考常考题型.

练习册系列答案
相关题目
17. 如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
 如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.下列说法:①球有1个面;②同一平面内的两点,可以确定一条直线;③两点之间,线段最短;④射线没有端点,其中不正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.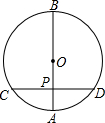 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
18. 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )| A. | 2,1,-2 | B. | -1,2,-2 | C. | -1,-2,2 | D. | -2,1,2 |
19.下列实数中无理数是( )
| A. | 0 | B. | 3 | C. | π | D. | $\sqrt{4}$ |
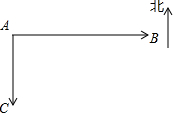 如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.
如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.