题目内容
请阅读下列材料:
=
-
,
+=
-
,
=
-
,…,所以
+
+
+
=1-
+
-
+
-
+
-
=1-
列问题:
(1)若n为正整数,请你猜想
= ;
(2)
+
+
+…+
= ;
化简:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 2 |
+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
列问题:
(1)若n为正整数,请你猜想
| 1 |
| n(n+1) |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
化简:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
考点:规律型:数字的变化类
专题:
分析:(1)分子是1,分母是连续两个自然数的乘积可以拆成两个分子是1,分母是这两个自然数的分数的差,由此规律得出答案即可;
(2)利用发现的规律拆分抵消计算即可.
(2)利用发现的规律拆分抵消计算即可.
解答:解:(1)若
=
-
;
(2)
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
;
化简:
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
=1-
| 1 |
| 10 |
=
| 9 |
| 10 |
化简:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
点评:此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,C,D是线段AB上的两点,E是AC的中点,F是BD是中点,若EF=a,CD=b,则AB的长( )
如图,C,D是线段AB上的两点,E是AC的中点,F是BD是中点,若EF=a,CD=b,则AB的长( )| A、a-b | B、a+b |
| C、2a-b | D、2a+b |
 如图表示的是某种摩托车的油箱中剩余量y(升)与摩托车行驶路程x(千米)之间的关系.由图象可知,摩托车最多装
如图表示的是某种摩托车的油箱中剩余量y(升)与摩托车行驶路程x(千米)之间的关系.由图象可知,摩托车最多装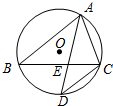 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.