题目内容
4.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A($\sqrt{3}$,0)、B(3$\sqrt{3}$,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2$\sqrt{5}-2$ | C. | 2$\sqrt{7}-2$ | D. | 2$\sqrt{10}-2$ |
分析 作圆,求出半径和PC的长度,判出点D只有在CP上时CD最短,CD=CP-DP求解.
解答 解:作圆,使∠ADB=60°,设圆心为P,连结PA、PB、PC,PE⊥AB于E,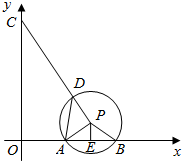 如图所示:
如图所示:
∵A($\sqrt{3}$,0)、B(3$\sqrt{3}$,0),
∴E(2$\sqrt{3}$,0)
又∠ADB=60°,
∴∠APB=120°,
∴PE=1,PA=2PE=2,
∴P(2$\sqrt{3}$,1),
∵C(0,5),
∴PC=$\sqrt{(2\sqrt{3})^{2}+(5-1)^{2}}$=2$\sqrt{7}$,
又∵PD=PA=2,
∴只有点D在线段PC上时,CD最短(点D在别的位置时构成△CDP)
∴CD最小值为:2$\sqrt{7}$-2.
故选:C.
点评 本题主要考查坐标与图形的性质,圆周角定理及勾股定理,解决本题的关键是判出点D只有在CP上时CD最短.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
14.下列各数是无理数的是( )
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | $\frac{3}{7}$ |
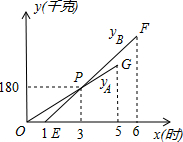 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: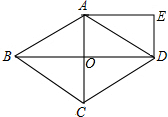 如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.
如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.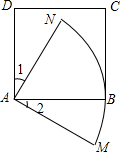 如图,在正方形ABCD中,以点A为圆心,AB长为半径作$\widehat{MN}$.若∠1=∠2,AB=2,则$\widehat{MN}$的长为π.
如图,在正方形ABCD中,以点A为圆心,AB长为半径作$\widehat{MN}$.若∠1=∠2,AB=2,则$\widehat{MN}$的长为π.