题目内容

1．计算：（π-4）0+|3-tan60°|-（$\frac{1}{2}$）-2+$\sqrt{27}$．

分析 直接利用零指数幂的性质以及绝对值的性质和特殊角的三角函数值、负整数指数幂的性质、二次根式的性质分别化简求出答案．

解答 解：原式=1+3-$\sqrt{3}$-4+3$\sqrt{3}$，
=2$\sqrt{3}$．

点评 此题主要考查了实数运算，正确掌握相关性质进而化简是解题关键．

练习册系列答案
相关题目
11．已知在△ABC中，AB=AC，AD是角平分线，点D在边BC上，设$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为（　　）
A．$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$B．$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$C．-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$D．-$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$
12．如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于30度．
9．下列计算正确的是（　　）
A．（xy）3=xy3B．x5÷x5=x
C．3x2•5x3=15x5D．5x2y3+2x2y3=10x4y9
16．“射击运动员射击一次，命中靶心”这个事件是（　　）
A．确定事件B．必然事件C．不可能事件D．不确定事件
4．在平面直角坐标系中，点O为坐标原点，点A、B、C的坐标分别为A（$\sqrt{3}$，0）、B（3$\sqrt{3}$，0）、C（0，5），点D在第一象限内，且∠ADB=60°，则线段CD的长的最小值是（　　）
A．2$\sqrt{3}$-2B．2$\sqrt{5}-2$C．2$\sqrt{7}-2$D．2$\sqrt{10}-2$
11．反比例函数y=$\frac{3-k}{x}$的图象位于第二、四象限，则k的取值范围是k＞3．
8．计算：
（1）（-$\frac{2}{3}$）×3÷6-（-32）；
（2）12×（$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$）．
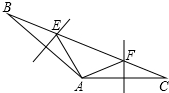9．如图，在△ABC中，AB和AC的垂直平分线分别交BC于E、F，若∠BAC=130°，则∠EAF=80°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网