题目内容
14．
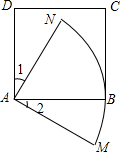如图，在正方形ABCD中，以点A为圆心，AB长为半径作$\widehat{MN}$．若∠1=∠2，AB=2，则$\widehat{MN}$的长为π．
分析 根据题意算出∠NAM=90°，AN=2，再根据弧长公式：l=$\frac{nπR}{180}$（弧长为l，圆心角度数为n，圆的半径为R）进行计算即可．
解答 解：∵四边形ABCD是正方形，
∴∠DAB=90°，
∵∠1=∠2，
∴∠NAM=90°，
∵以点A为圆心，AB长为半径作弧MN，AB=2，
∴AN=2，
∴弧MN的长为：l=$\frac{nπR}{180}$=$\frac{90π×2}{180}$=π，
故答案为π．
点评 本题主要考查了弧长计算，关键是熟练掌握弧长l=$\frac{nπR}{180}$的计算公式．
练习册系列答案
阅读快车系列答案
相关题目
4．在平面直角坐标系中，点O为坐标原点，点A、B、C的坐标分别为A（$\sqrt{3}$，0）、B（3$\sqrt{3}$，0）、C（0，5），点D在第一象限内，且∠ADB=60°，则线段CD的长的最小值是（ ）
| A． | 2$\sqrt{3}$-2 | B． | 2$\sqrt{5}-2$ | C． | 2$\sqrt{7}-2$ | D． | 2$\sqrt{10}-2$ |
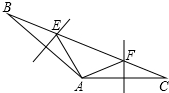如图，在△ABC中，AB和AC的垂直平分线分别交BC于E、F，若∠BAC=130°，则∠EAF=80°．