题目内容
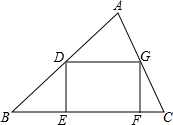已知在△ABC中，BC=5，BC边上的高为4，矩形DEFG顶点D、G分别在AB、AC上，点E、F在BC上且DE：EF=3：4，求矩形的边DE、EF的长．考点：相似三角形的判定与性质,矩形的性质
专题：常规题型
分析：作AH⊥BC于H点，可得△ADG∽△ABC，△BDE∽△BAH，根据相似三角形对应边比例等于相似比可解题．
解答：解：作AH⊥BC于H点，
∵四边形DEFG为矩形，
∴△ADG∽△ABC，△BDE∽△BAH，
∴
=
，
=
，
∵
+
=1，
∴
+
=1，即
+
=1，
∵DE：EF=3：4
∴EF=
，DE=
．
∵四边形DEFG为矩形，
∴△ADG∽△ABC，△BDE∽△BAH，
∴
| DE |
| AH |
| BD |
| AB |
| DG |
| BC |
| AD |
| AB |
∵
| BD |
| AB |
| AD |
| AB |
∴
| DE |
| AH |
| DG |
| BC |
| DE |
| 4 |
| DG |
| 5 |
∵DE：EF=3：4
∴EF=
| 80 |
| 31 |
| 60 |
| 31 |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
相关题目
下列代数式的值中，一定是正数的是（ ）
| A、（x+1）2 |
| B、|x+1|+2 |
| C、（-x）2 |
| D、-x2+1 |
如图，已知在△ABC中，AB=AC，AD是BC边上的高，P是AB边上的一点，试在高AD上找一点E，使得△PEB的周长最短．
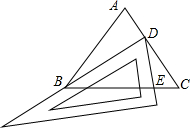如图，在等边△ABC中，D是AC上一动点（与A、C不重合），使一块三角板的60°角的顶点与点D重合，并且斜边始终经过点B，一直角边与△ABC的边BC相交于点E．
尺规作图：（保留作图痕迹，不写作法）已知：如图，线段m，n，∠α．求作：△ABC，使得∠A=∠α，AB=m，AC=n．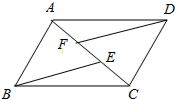
如图，AD=BC，AE=CF，DF=BE，找出图中一对全等的三角形，并说明理由．