题目内容
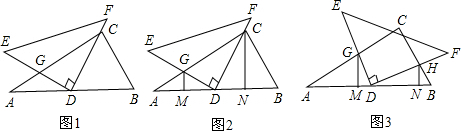
图中是一副三角板,45°的三角板Rt△DEF的直角顶点D恰好在30°的三角板Rt△ABC斜边AB的中点处,∠A=30°,∠E=45°,∠EDF=∠ACB=90°,DE交AC于点G.
(1)如图1,当DF经过点C时,求证:△BCD为等边三角形.
(2)如图2,当DF经过点C时,作GM⊥AB于M,CN⊥AB于N,求证:AM=DN.
(3)如图3,当DF∥AC 时, DF 交BC于H,作GM⊥AB于M,HN⊥AB于N,请问结论AM=DN是否成立?若成立,请你给出证明;若不成立,请说明理由.
(1)如图1,当DF经过点C时,求证:△BCD为等边三角形.
(2)如图2,当DF经过点C时,作GM⊥AB于M,CN⊥AB于N,求证:AM=DN.
(3)如图3,当DF∥AC

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等腰三角形中一个角为60°,即可判定等边三角形;
(2)根据等边三角形的性质可以解本题;
(3)易证△ADG≌△DBH,可证△AMG≌△DNH即可解题.
(2)根据等边三角形的性质可以解本题;
(3)易证△ADG≌△DBH,可证△AMG≌△DNH即可解题.
解答:证明:(1)∵∠A=30°,∠ACB=90°,D是AB的中点.
∴CD=BD,∠B=60°
∴△BCD是等边三角形.
(2)
证明:∵△BCD是等边三角形,CN⊥DB,
∴DN=
BD
∵∠EDF=90°,△BCD是等边三角形.
∴∠ADG=30°,而∠A=30°.
∴GA=GD.
∵GM⊥AB
∴AM=
AD,
又∵AD=DB
∴AM=DN
(3)
∵DF∥AC
∴∠BDH=∠A=30°,∠AGD=∠GDH=90°,
∴∠ADG=60°
∴∠ADG=∠B=60°.
在△ADG和△DBH中,
,
∴△ADG≌△DBH(ASA)
∴AG=DH,
又∵∠BDH=∠A,GM⊥AB,HN⊥AB,
∴∠AMG=∠DNH
在△AMG和△DNH中,
,
∴△AMG≌△DNH(AAS).
∴AM=DN.
∴CD=BD,∠B=60°
∴△BCD是等边三角形.
(2)

证明:∵△BCD是等边三角形,CN⊥DB,
∴DN=
| 1 |
| 2 |
∵∠EDF=90°,△BCD是等边三角形.
∴∠ADG=30°,而∠A=30°.
∴GA=GD.
∵GM⊥AB
∴AM=
| 1 |
| 2 |
又∵AD=DB
∴AM=DN
(3)

∵DF∥AC
∴∠BDH=∠A=30°,∠AGD=∠GDH=90°,
∴∠ADG=60°
∴∠ADG=∠B=60°.
在△ADG和△DBH中,
|
∴△ADG≌△DBH(ASA)
∴AG=DH,
又∵∠BDH=∠A,GM⊥AB,HN⊥AB,
∴∠AMG=∠DNH
在△AMG和△DNH中,
|
∴△AMG≌△DNH(AAS).
∴AM=DN.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADG≌△DBH是解题的关键.

练习册系列答案
相关题目
比较-2,0,-(-2),-3的大小,正确的是( )
| A、0>-3>-(-2)>-2 |
| B、-(-2)>-3>-2>0 |
| C、-(-2 )>0>-2>-3 |
| D、-3>-(-2)>-2>0 |
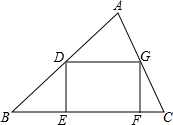 已知在△ABC中,BC=5,BC边上的高为4,矩形DEFG顶点D、G分别在AB、AC上,点E、F在BC上且DE:EF=3:4,求矩形的边DE、EF的长.
已知在△ABC中,BC=5,BC边上的高为4,矩形DEFG顶点D、G分别在AB、AC上,点E、F在BC上且DE:EF=3:4,求矩形的边DE、EF的长. 如图,在△ABC中,∠ACB=90°,CD是斜边上的高线,CE平分∠ACB,且∠B=30°,求∠DCE的度数.
如图,在△ABC中,∠ACB=90°,CD是斜边上的高线,CE平分∠ACB,且∠B=30°,求∠DCE的度数. 已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)
已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)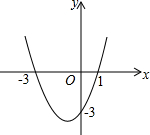 二次函数y=ax2+bx+c(a≠0)的图象如图所示,求:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,求: