题目内容
已知△ABC∽△DEF,它们的面积比为4:9,AM是△ABC的角平分线,DN是△DEF的角平分线.
(1)求证:△ABM∽△DEN;
(2)求
的值.
(1)求证:△ABM∽△DEN;
(2)求
| AM |
| DN |
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)根据△ABC∽△DEF,可得∠B=∠E,∠BAC=∠EDF,根据AM、AN是角平分线即可证明△ABM∽△DEN;
(2)根据相似三角形面积比为相似比的平方即可解题.
(2)根据相似三角形面积比为相似比的平方即可解题.
解答:解:(1)∵△ABC∽△DEF,
∴∠B=∠E,∠BAC=∠EDF,
∵AM是△ABC的角平分线,DN是△DEF的角平分线.
∴∠BAM=∠CAN,
∴△ABM∽△DEN;
(2)∵△ABC和△DEF的面积比为4:9,
∴AB:DE=2:3,
∴
=
=
.
∴∠B=∠E,∠BAC=∠EDF,
∵AM是△ABC的角平分线,DN是△DEF的角平分线.
∴∠BAM=∠CAN,
∴△ABM∽△DEN;
(2)∵△ABC和△DEF的面积比为4:9,
∴AB:DE=2:3,
∴
| AM |
| DN |
| AB |
| DE |
| 2 |
| 3 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,考查了相似三角形面积比为相似比平方的性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
比较-2,0,-(-2),-3的大小,正确的是( )
| A、0>-3>-(-2)>-2 |
| B、-(-2)>-3>-2>0 |
| C、-(-2 )>0>-2>-3 |
| D、-3>-(-2)>-2>0 |
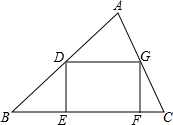 已知在△ABC中,BC=5,BC边上的高为4,矩形DEFG顶点D、G分别在AB、AC上,点E、F在BC上且DE:EF=3:4,求矩形的边DE、EF的长.
已知在△ABC中,BC=5,BC边上的高为4,矩形DEFG顶点D、G分别在AB、AC上,点E、F在BC上且DE:EF=3:4,求矩形的边DE、EF的长.
 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.
如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.