题目内容
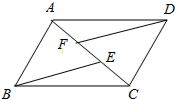如图，AD=BC，AE=CF，DF=BE，找出图中一对全等的三角形，并说明理由．考点：全等三角形的判定
专题：开放型
分析：求出AF=CE，然后利用“边边边”证明△ADF和△CBE全等即可．
解答：解：△ADF和△CBE全等．
理由如下：∵AE=CF，
∴AE-EF=CF-EF，
即AF=CE，
在△ADF和△CBE中，
，
∴△ADF≌△CBE（SSS）．
理由如下：∵AE=CF，
∴AE-EF=CF-EF，
即AF=CE，
在△ADF和△CBE中，
|
∴△ADF≌△CBE（SSS）．
点评：本题考查了全等三角形的判定，熟练掌握三角形全等的判定方法是解题的关键，难点在于求出AF=CE．
练习册系列答案
名校通行证有效作业系列答案
相关题目
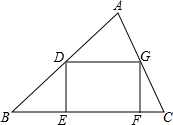已知在△ABC中，BC=5，BC边上的高为4，矩形DEFG顶点D、G分别在AB、AC上，点E、F在BC上且DE：EF=3：4，求矩形的边DE、EF的长．
如图，已知∠AOB及点C、D两点，请利用直尺和圆规作一点P，使得点P到射线OA、OB的距离相等，且P点到点C、D的距离也相等．
如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=13cm，BC=14cm，CA=9cm，求：AF、BD、CF的长．
如图，在△ABC中，∠ACB=90°，CD是斜边上的高线，CE平分∠ACB，且∠B=30°，求∠DCE的度数．