题目内容
20. 如图,可以得出不等式组$\left\{\begin{array}{l}{ax+b<0}\\{cx+d>0}\end{array}\right.$的解集是( )
如图,可以得出不等式组$\left\{\begin{array}{l}{ax+b<0}\\{cx+d>0}\end{array}\right.$的解集是( )| A. | x<-1 | B. | -1<x<0 | C. | -1<x<4 | D. | x>4 |
分析 根据直线y=ax+b交x轴于点(4,0),直线y=cx+d交x轴于点(-1,0),再结合图象即可得出两不等式的解集,进而得出答案.
解答 解:∵直线y=ax+b交x轴于点(4,0),
∴ax+b<0的解集为:x>4,
∵直线y=cx+d交x轴于点(-1,0),
∴cx+d>0的解集为:x>-1,
∴不等式组$\left\{\begin{array}{l}{ax+b<0}\\{cx+d>0}\end{array}\right.$的解集是:x>4.
故选D.
点评 本题考查了一次函数与一元一次不等式,属于基础题,关键是正确根据图象解题.

练习册系列答案
相关题目
10.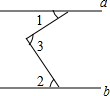 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )| A. | 100° | B. | 90° | C. | 70° | D. | 50° |
10.下列运算中,正确的是( )
| A. | 4x+3y=7xy | B. | 3x2+2=5x2 | C. | 6xy-4xy=2xy | D. | 5x2-x2=4 |

