题目内容
19．
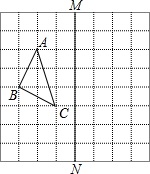如图，在正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．（1）在图中作出△ABC关于直线MN对称的△A′B′C′；
（2）在（1）的结果下，连接AA′，CC′，求四边形AA′C′C的面积．
分析 （1）根据轴对称的性质作出△ABC关于直线MN对称的△A′B′C′即可；
（2）根据梯形的面积公式求出梯形AA′C′C的面积即可．
解答 
解：（1）如图所示；
（2）∵由图得四边形AA′C′C的面积是等腰梯形，CC′=2，AA′=4，高是3，
∴S四边形AA′C′C=$\frac{1}{2}$（AA′+CC′）×3=$\frac{1}{2}$（4+2）×3=9．
点评 本题考查的是作图-轴对称变换，熟知轴对称图形的作法是解答此题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
9．下列计算错误的是（ ）
| A． | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$ | B． | $\frac{a-b}{b-a}$=-1 | C． | $\frac{2a+b}{a+b}$=2 | D． | $\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$ |
如图，在△ABC中，AD为边BC上的中线，延长AD的到E，使得DE=AD，连接BE
14．已知一个三角形的周长为18cm，且它的角平分线的交点到一边的距离是2.5cm，则这个三角形的面积是（ ）
| A． | 22.5cm2 | B． | 19cm2 | C． | 21cm2 | D． | 23.5cm2 |
如图，∠A=90°，E为BC上的一点，A点和E点关于BD的对称，B点、C点关于DE对称，求∠ABC和∠C的度数．