题目内容
11. 如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
分析 根据轴对称的性质可得∠ABD=∠EBD,∠C=∠DBC,进而可得∠ABC=2∠ABD=2∠DBE,∠ABC=2∠C,再根据∠A=90°,可得∠ABC+∠BCD=90°,进而可得答案.
解答 解:∵A点和E点关于BD的对称,
∴∠ABD=∠EBD,
即∠ABC=2∠ABD=2∠DBE,
∵B点、C点关于DE对称,
∴∠C=∠DBC,
∴∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠BCD=90°,
∴∠ABC=60°,∠C=30°.
点评 此题主要考查了轴对称的性质,以及直角三角形的性质,关键是掌握如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.已知点M(a,3),B(2,b)关于x轴对称,则(a+b)2014的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
16. 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )| A. | 0根 | B. | 1根 | C. | 2根 | D. | 3根 |
1.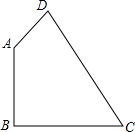 在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
 在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
 如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,
如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,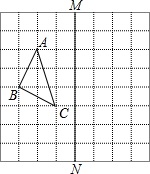 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).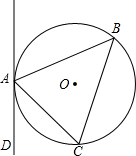 如图,△ABC是⊙O的内接三角形,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
如图,△ABC是⊙O的内接三角形,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.