题目内容
9.几组数据①12,35,36;②1,1,$\sqrt{2}$;③32,42,52;④5,12,13,可以作为直角三角形三边的是②④.(填序号)分析 根据勾股定理的逆定理,求出两小边的平方和,再求出最大边的平方,看是否相等,即可得出答案.
解答 解:①∵122+352≠362,∴不能构成直角三角形;
②∵12+12=($\sqrt{2}$)2,∴能构成直角三角形;
③∵(32)2+(42)2≠(52)2,∴不能构成直角三角形;
④∵52+122=132,∴能构成直角三角形.
故答案为②④.
点评 本题考查了对勾股定理的逆定理的运用,勾股定理的逆定理是:如果一个三角形的三边分别是a、b、c(c最大)满足a2+b2=c2,则三角形是直角三角形.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.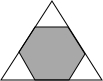 如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )
如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )
 如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )
如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
14.(-0.7)2的平方根是( )
| A. | 0.49 | B. | -0.7 | C. | 0.7 | D. | ±0.7 |
1.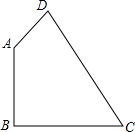 在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
 在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )
在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,则∠DAB的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
18.下列函数关系式中,一定是反比例函数的是( )
| A. | y=$\frac{6}{x}$ | B. | y=-$\frac{12}{x}$+1 | C. | y=$\frac{k}{x}$ | D. | y=-$\frac{5}{2x}$-1 |
19.已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$,则$\frac{x+3y-z}{2x-y+z}$的值是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
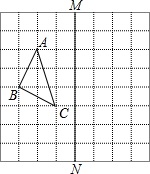 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).