题目内容
14. 如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.(1)若∠B=30°,∠C=70°,求∠DAE的度数;
(2)△ABC中,若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系,并说明理由.
分析 (1)首先根据三角形的内角和定理,求出∠BAC的度数;然后根据角平分线的性质,求出∠BAE、∠CAE的度数是多少;最后根据三角形的外角的性质,求出∠AED的度数,进而求出∠DAE的度数是多少即可.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE=$\frac{β-α}{2}$,然后根据(1)中求解的方法,证明猜想的正确性即可.
解答 解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°-30°-70°=80°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=80°÷2=40°,
∵∠AED=∠B+∠BAE=30°+40°=70°,
∴∠DAE=90°-70°=20°.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE=$\frac{β-α}{2}$,
证明∵∠B=α,∠C=β,
∴∠BAC=180°-α-β,
∵AE平分∠BAC,
∴∠BAE=∠CAE=(180°-α-β)÷2=90°-$\frac{α+β}{2}$,
∵∠AED=∠B+∠BAE=α+(90°-$\frac{α+β}{2}$)=90°+$\frac{α-β}{2}$,
∴∠DAE=90°-(90°+$\frac{α-β}{2}$)=$\frac{β-α}{2}$.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质,要熟练掌握,解答此题的关键是要明确:三角形的外角等于和它不相邻的两个内角的和.
(3)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的角平分线把这个角分成两个大小相同的角.

练习册系列答案
相关题目
10. 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
2.某校将举行一场“汉字电脑录入大赛”,要求各班推选一名同学参加比赛.为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.7,根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
3.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | ∠A=∠B,∠C=∠D | C. | AB=CD,AD=BC | D. | AB=AD,CB=CD |
 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.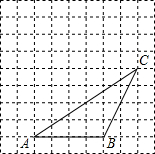 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.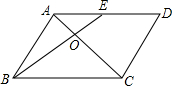 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,若AO=4,则AC=12.
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,若AO=4,则AC=12.