题目内容
10. 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
分析 首先在$\widehat{AC}$上取点D,连接AD,CD,由圆周角定理即可求得∠D的度数,然后由圆的内接四边形的性质,求得∠ABC的度数.
解答  解:如图,在优弧$\widehat{AC}$上取点D,连接AD,CD,
解:如图,在优弧$\widehat{AC}$上取点D,连接AD,CD,
∵∠AOC=100°,
∴∠ADC=$\frac{1}{2}$∠AOC=50°,
∴∠ABC=180°-∠ADC=130°.
故选D.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
1.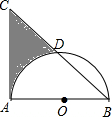 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )| A. | 24-4π | B. | 32-4π | C. | 32-8π | D. | 16 |
5. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
2.下列几何图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 正方形 |
19. 一个几何体的表面展开图如图所示,则这个几何体是( )
一个几何体的表面展开图如图所示,则这个几何体是( )
 一个几何体的表面展开图如图所示,则这个几何体是( )
一个几何体的表面展开图如图所示,则这个几何体是( )| A. | 四棱锥 | B. | 四棱柱 | C. | 三棱锥 | D. | 三棱柱 |
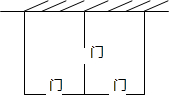 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2. 如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.