题目内容
5. 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)
分析 根据在Rt△ACD中,tan∠ACD=$\frac{AD}{CD}$,求出AD的值,再根据在Rt△BCD中,tan∠BCD=$\frac{BD}{CD}$,求出BD的值,最后根据AB=AD+BD,即可求出答案.
解答 解:在Rt△ACD中,
∵tan∠ACD=$\frac{AD}{CD}$,
∴tan30°=$\frac{AD}{9}$,
∴$\frac{AD}{9}$=$\frac{\sqrt{3}}{3}$,
∴AD=3$\sqrt{3}$m,
在Rt△BCD中,
∵∠BCD=45°,
∴BD=CD=9m,
∴AB=AD+BD=3$\sqrt{3}$+9(m).
故答案为:3$\sqrt{3}$+9.
点评 此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
15.十边形的内角和为( )
| A. | 1260° | B. | 1440° | C. | 1620° | D. | 1800° |
20.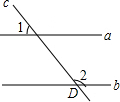 如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
 如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )| A. | 150° | B. | 130° | C. | 100° | D. | 50° |
10.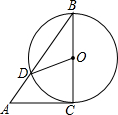 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )
 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为( )| A. | 70° | B. | 60° | C. | 55° | D. | 35° |
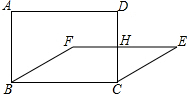 如图,若将四根木条钉成的矩形ABCD变形为?FBCE的形状,EF交CD于点H,已知AB=20cm,BC=30cm,当矩形ABCD的面积是?FBCE面积的2倍时,四边形FBCH的面积为(300-50$\sqrt{3}$)cm2.
如图,若将四根木条钉成的矩形ABCD变形为?FBCE的形状,EF交CD于点H,已知AB=20cm,BC=30cm,当矩形ABCD的面积是?FBCE面积的2倍时,四边形FBCH的面积为(300-50$\sqrt{3}$)cm2.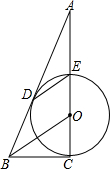 如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.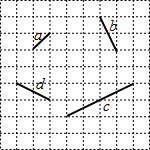 如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )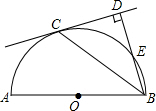 如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.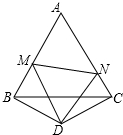 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.