题目内容
16.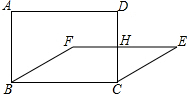 如图,若将四根木条钉成的矩形ABCD变形为?FBCE的形状,EF交CD于点H,已知AB=20cm,BC=30cm,当矩形ABCD的面积是?FBCE面积的2倍时,四边形FBCH的面积为(300-50$\sqrt{3}$)cm2.
如图,若将四根木条钉成的矩形ABCD变形为?FBCE的形状,EF交CD于点H,已知AB=20cm,BC=30cm,当矩形ABCD的面积是?FBCE面积的2倍时,四边形FBCH的面积为(300-50$\sqrt{3}$)cm2.
分析 根据矩形ABCD的面积是?FBCE面积的2倍,得出CH=$\frac{1}{2}$AB,再由三角函数即可求出∠E的度数,解直角三角函数求得EH的值,进而求得FH的值,然后根据梯形的面积公式即可求得.
解答 解:∵四边形ABCD是矩形,
∴DC⊥BC,
∵?FBCE中,EF∥BC,
∴DC⊥EF,
根据题意得:AB=CD=BF=CE,AD=BC=EF,?FBCE面积=BC•CH=$\frac{1}{2}$BC•AB,
∴CH=$\frac{1}{2}$AB,
∵CE=BF=AB,
∴CH=$\frac{1}{2}$CE,
∴sinE=$\frac{CH}{CE}$=$\frac{1}{2}$,
∴∠E=30°,
∴EH=cos30°•CE=$\frac{\sqrt{3}}{2}$×20=10$\sqrt{3}$cm,
∴FH=EF-HE=30-10$\sqrt{3}$,
∴四边形FBCH的面积=$\frac{1}{2}$(FH+BC)•CH=$\frac{1}{2}$(30-10$\sqrt{3}$+30)•10=(300-50$\sqrt{3}$)cm2,
故答案为(300-50$\sqrt{3}$)cm2.
点评 本题考查了平行四边形的性质、矩形的性质、面积的计算以及三角函数;熟练掌握平行四边形和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
6.某市70%的家庭年收入不少于3万元,下面一定不少于3万元的是( )
| A. | 年收入的平均数 | B. | 年收入的中位数 | ||
| C. | 年收入的众数 | D. | 年收入的平均数和众数 |
4. 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{10}$ |
1.2014年德州市农村中小学校含标准化工程开工学校项目356个,开工面积56.2万平方米,开式面积量创历年最高,56.2万平方米用科学记数法表示正确的是( )
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×104m2 |
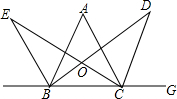 如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系.
如图所示,在△ABC中,CD、BE是△ABC的外角平分线,BD为∠ABC的平分线,CE为∠ACB的平分线,BE、CE交于点E,BD、CD交于点D,试探索∠D与∠E的关系. 如图,∠1=∠2,∠3=∠4,求证:AC=AD.
如图,∠1=∠2,∠3=∠4,求证:AC=AD. 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)