题目内容
6.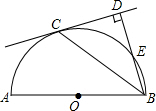 如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.(1)求证:CD是半圆O的切线.
(2)若DC=4$\sqrt{3}$,BE=8,求$\widehat{AC}$的长(结果保留π).
分析 (1)首先连接OC,由OB=OC,BC平分∠DBA,易证得OC∥BD,又由BD⊥CD,即可证得结论;
(2)首先根据切割线定理求得BD,然后根据勾股定理求得BC,连接AC,通过证得△ABC∽△CBD,然后由相似三角形的对应边成比例,求得AB,通过解直角三角形求得∠ABC的度数,进而求得∠AOC的度数,最后根据弧长公式求得即可.
解答  解:(1)CD与半圆O相切.
解:(1)CD与半圆O相切.
理由:连接OC,
∵OB=OC,
∴∠1=∠2,
∵BC平分∠DBA,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥BD,
∵BD⊥CD,
∴OC⊥CD,
∵C是半圆O上的一点,
∴CD与半圆O相切.
(2)连接AC,
∵CD是切线,
∴CD2=DE•BD,
∵DC=4$\sqrt{3}$,BE=8,
设BD=x,则(4$\sqrt{3}$)2=x(x-8),
解得x=12,
∴BD=12,
∵∠BDC=90°,
∴BC=$\sqrt{D{C}^{2}+B{D}^{2}}$=8$\sqrt{3}$,
∵AB是直径,
∴∠ACB=90°=∠BDC,
∵∠BDC=∠ABC,
∴△CDB∽△ACB,
∴$\frac{AB}{BC}$=$\frac{BC}{BD}$,即$\frac{AB}{8\sqrt{3}}$=$\frac{8\sqrt{3}}{12}$,
∴AB=16,
∵sin∠3=$\frac{CD}{BC}$=$\frac{4\sqrt{3}}{8\sqrt{3}}$=$\frac{1}{2}$,
∴∠3=30°,
∴∠2=30°
∴∠AOC=60°,
∴$\widehat{AC}$的长=$\frac{60×π×8}{180}$=$\frac{8}{3}$π.
点评 此题考查了切线的判定、圆周角定理、等腰三角的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

 如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )
如图,用一根长40cm长的铁丝剪成两段,分别作成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{10}$ |
 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是3$\sqrt{3}$+9m(结果保留根号)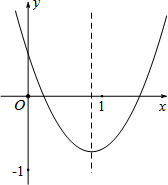 已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2-4ac,a+b+c,a-b+c,2a+b中,其值为正的式子的个数为( )