题目内容
17.已知△ABC的三边a=m-n(m>n>0),b=m+n,c=2$\sqrt{mn}$.(1)求证:△ABC是直角三角形;
(2)利用第(1)题的结论,写出两组m,n的值,要求三角形的边长均为整数.
分析 (1)根据勾股定理的逆定理即可得到结论;
(2)根据(1)题的结论即可得到结果.
解答 解:(1)∵a=m-n(m>n>0),b=m+n,c=2$\sqrt{mn}$,
∴(m-n)2+(2$\sqrt{mn}$)2=m2+n2-2mn+4mn=(m+n)2,
∴△ABC是直角三角形;
(2)当m=4,n=1时,三角形的边长为3,4,5;
当m=9,n=4时,三角形的边长为5,12,13.
点评 本题考查了勾股定理的逆定理的应用,在应用时注意是两较短边的平方和等于最长边的平方.

练习册系列答案
相关题目
5.已知数349028用四舍五入法保留两个有效数字约是3.5×105,则所得近似数精确到( )
| A. | 十位 | B. | 千位 | C. | 万位 | D. | 百位 |
7.化简-$\frac{2x}{{x}^{2}-1}$$+\frac{1}{x+1}$的结果为( )
| A. | -x+1 | B. | -x-1 | C. | -$\frac{1}{x-1}$ | D. | $\frac{1}{x-1}$ |
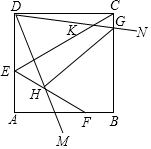 正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.
正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.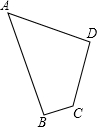 如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.