题目内容
16. 如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.
如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.
分析 在Rt△AOB、Rt△DOC中分别表示出AO2、DO2,从而在Rt△ADO中利用勾股定理即可得出AD的长度.
解答  解:在Rt△AOB中,AO2=AB2-BO2;
解:在Rt△AOB中,AO2=AB2-BO2;
Rt△DOC中可得:DO2=DC2-CO2;
∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=18,
即可得AD=$\sqrt{18}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 此题考查了勾股定理的知识,解答本题的关键是在Rt△AOB、Rt△DOC中分别表示出AO2、DO2,需要我们熟练掌握勾股定理的表达形式.

练习册系列答案
相关题目
7.若a=2016,b=-2017,则分式1+$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$÷$\frac{1}{a}$的值是( )
| A. | 2016 | B. | 0 | C. | -2017 | D. | 4034 |
1.若“!”是一种数学运算符号,并1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则$\frac{50!}{48!}$的值为( )
| A. | 0.2! | B. | 2450 | C. | $\frac{25}{24}$ | D. | 49! |
 在如图所示的四边形ABCD中,AB=12,BC=13,CD=4,AD=3,AD⊥CD,求这个四边形ABCD的面积.
在如图所示的四边形ABCD中,AB=12,BC=13,CD=4,AD=3,AD⊥CD,求这个四边形ABCD的面积.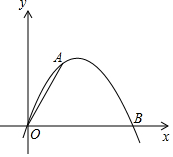 如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0).
如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0).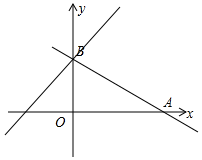 如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.
如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.