题目内容
4.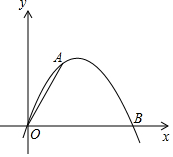 如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0).
如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0).(1)求a,b的值;
(2)求该二次函数的图象的顶点坐标;
(3)C是该二次函数的图象上A,B两点之间的一个动点,点C的横坐标为x,写出四边形OBCA的面积S关于点C的横坐标x的函数解析式,并求出S的最大值.
分析 (1)把A点和B点坐标分别代入y=ax2+bx得$\left\{\begin{array}{l}{4a+2b=4}\\{36a+6b=0}\end{array}\right.$,然后给解方程组即可得到a和b的值;
(2)有(1)得到抛物线解析式为y=-$\frac{1}{2}$x2+3x,然后利用配方法把一般式配成顶点式,从而得到抛物线的顶点坐标;
(3)作AM⊥x轴于点M,CN⊥x轴于N,如图,设C(x,-$\frac{1}{2}$x2+3x),利用S四边形OBCA=S△AOM+S梯形AMNC+S△CNB可得到S与x的关系,然后利用二次函数的性质求S的最大值.
解答 解:(1)把A(2,4)和B(6,0)分别代入y=ax2+bx得$\left\{\begin{array}{l}{4a+2b=4}\\{36a+6b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=3}\end{array}\right.$;
(2)抛物线解析式为y=-$\frac{1}{2}$x2+3x
因为y=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,
所以抛物线的顶点坐标为(3,$\frac{9}{2}$);
(3)作AM⊥x轴于点M,CN⊥x轴于N,如图,设C(x,-$\frac{1}{2}$x2+3x),
∵S四边形OBCA=S△AOM+S梯形AMNC+S△CNB,
∴S=$\frac{1}{2}$•2•4+$\frac{1}{2}$(-$\frac{1}{2}$x2+3x+4)(x-2)+$\frac{1}{2}$•(6-x)•(-$\frac{1}{2}$x2+3x)
=-x2+8x
=-(x-4)2+16(2<x<6),
当x=4时,S有最大值,最大值为16.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会运用待定系数法求抛物线的解析式;能运用分割法求不规则图形的面积.

| A. | (-2,2) | B. | (1,5) | C. | (1,-1) | D. | (4,2) |
(1)(-3)+(-4)-(+11)-(-19)
(2)10+2÷$\frac{1}{3}$×(-2)
(3)10+8×(-$\frac{1}{2}$)2-2÷$\frac{1}{5}$.
| A. | 3(x+1)2=2(x-1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2+2x=x2 |
 如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.
如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.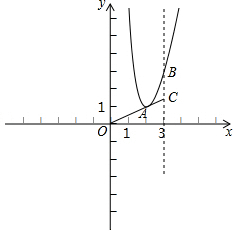 如图,在平面直角坐标系内,抛物线y=2x2+bx+c的顶点为A(2,1),同时与直线x=3交于点B,连接OA并延长与直线x=3交于点C.
如图,在平面直角坐标系内,抛物线y=2x2+bx+c的顶点为A(2,1),同时与直线x=3交于点B,连接OA并延长与直线x=3交于点C.