题目内容
六一儿童节,宝宝、心心、豆豆和他们的妈妈在电视台做亲子的游戏,三位妈妈、三个孩子都蒙上眼睛,在场中走了30s后,妈妈开始找孩子,直到每一位妈妈都找到孩子为止,当然游戏不准暗示.假定每位妈妈找到每一位孩子的可能性相同.
(1)求三位妈妈都找到自己孩子的概率.
(2)求恰有一位妈妈找到自己孩子的概率.
(1)求三位妈妈都找到自己孩子的概率.
(2)求恰有一位妈妈找到自己孩子的概率.
考点:列表法与树状图法
专题:
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与三位妈妈都找到自己孩子的情况,再利用概率公式即可求得答案;
(2)根据(1)中的树状图求得恰有一位妈妈找到自己孩子的情况,再利用概率公式即可求得答案.
(2)根据(1)中的树状图求得恰有一位妈妈找到自己孩子的情况,再利用概率公式即可求得答案.
解答:解:(1)画树状图得:

∵共有27种等可能的结果,三位妈妈都找到自己孩子的只有1种情况,
∴三位妈妈都找到自己孩子的概率为:
;
(2)∵恰有一位妈妈找到自己孩子的有12种情况,
∴恰有一位妈妈找到自己孩子的概率为:
=
.

∵共有27种等可能的结果,三位妈妈都找到自己孩子的只有1种情况,
∴三位妈妈都找到自己孩子的概率为:
| 1 |
| 27 |
(2)∵恰有一位妈妈找到自己孩子的有12种情况,
∴恰有一位妈妈找到自己孩子的概率为:
| 12 |
| 27 |
| 4 |
| 9 |
点评:此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
把160000用科学记数法表示为( )
| A、16×104 |
| B、1.6×104 |
| C、1.6×105 |
| D、0.16×104 |
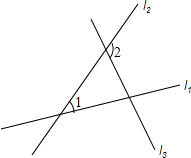 如图,直线l1、l2、l3两两相交,则对于∠1、∠2,下列说法正确的是( )
如图,直线l1、l2、l3两两相交,则对于∠1、∠2,下列说法正确的是( )| A、∠1、∠2是直线l1、l2被直线l3所截得的同位角 |
| B、∠1、∠2是直线l1、l3被直线l2所截得的同位角 |
| C、∠1、∠2是直线l2、l3被直线l1所截得的同位角 |
| D、∠1、∠2是直线l1、l2被直线l3所截得的同旁内角 |
以下说法正确的是( )
| A、50个同学中,就很可能有2个同学的生日相同 |
| B、一个游戏的中奖率是1%,买100张奖券,一定命中奖 |
| C、一副扑克牌中,随意抽取一张是红桃K,这是必然事件 |
| D、一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是1 |
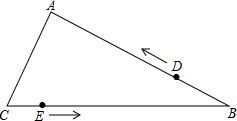 如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.
如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值. 如图:
如图: 如图,菱形ABCD中,对角线AC与BD相交于O,过A作AE∥BD,过O作OE∥AB,OE与AE相交于E,请问,四边形AODE是什么特殊的四边形?并证明你的结论.
如图,菱形ABCD中,对角线AC与BD相交于O,过A作AE∥BD,过O作OE∥AB,OE与AE相交于E,请问,四边形AODE是什么特殊的四边形?并证明你的结论.